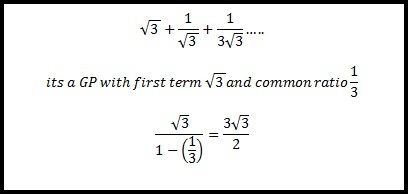Divided by three

Algebra Level 3

3 + 1 3 + 1 3 3 + 1 9 3 + . . . . . . . . . = a b c \large \sqrt{3} + \frac{1}{ \sqrt{3} } + \frac{1}{3 \sqrt{3} } + \frac{1}{ 9 \sqrt{3} } + ......... = \frac{a \sqrt{b} }{ c }

Where a and c are positive coprime integers and b is a square free integer.

Find a + b + c a + b + c .

This problem is a part of the sets - 1's & 2's & QuEsTiOnS .


The answer is 8.

Sakanksha Deo by Sakanksha Deo , 23, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

4 solutions

Ramesh Goenka
Mar 16, 2015

8 Helpful 0 Interesting 0 Brilliant 0 Confused
Gamal Sultan
Mar 22, 2015

The given series is an infinite geometric one

The first term is square root of 3 , and the common ratio is 1/3

The sum = (square root of 3)/(1 - 1/3) = 3(square root of 3)/2

a = 3, b = 3 , c = 2

a + b + c = 3 + 3 + 2 = 8

1 Helpful 0 Interesting 0 Brilliant 0 Confused
Somesh Singh
Mar 22, 2015

well the answer comes out to be 3sqrt(3)/2.....SO the sum is 8 but it can also be interpreted as sqrt(27)/2 so now the sum would be: 1+27+2=30!!! in fact, infinitely many integer solutions are possible...

0 Helpful 0 Interesting 0 Brilliant 0 Confused
David Holcer
Mar 17, 2015

s=series 2/3s=root 3 s=(3 root 3)/2

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...