Dividing triangle
In the given , the red areas are equal, and , where , and are coprime positive integers. Find .
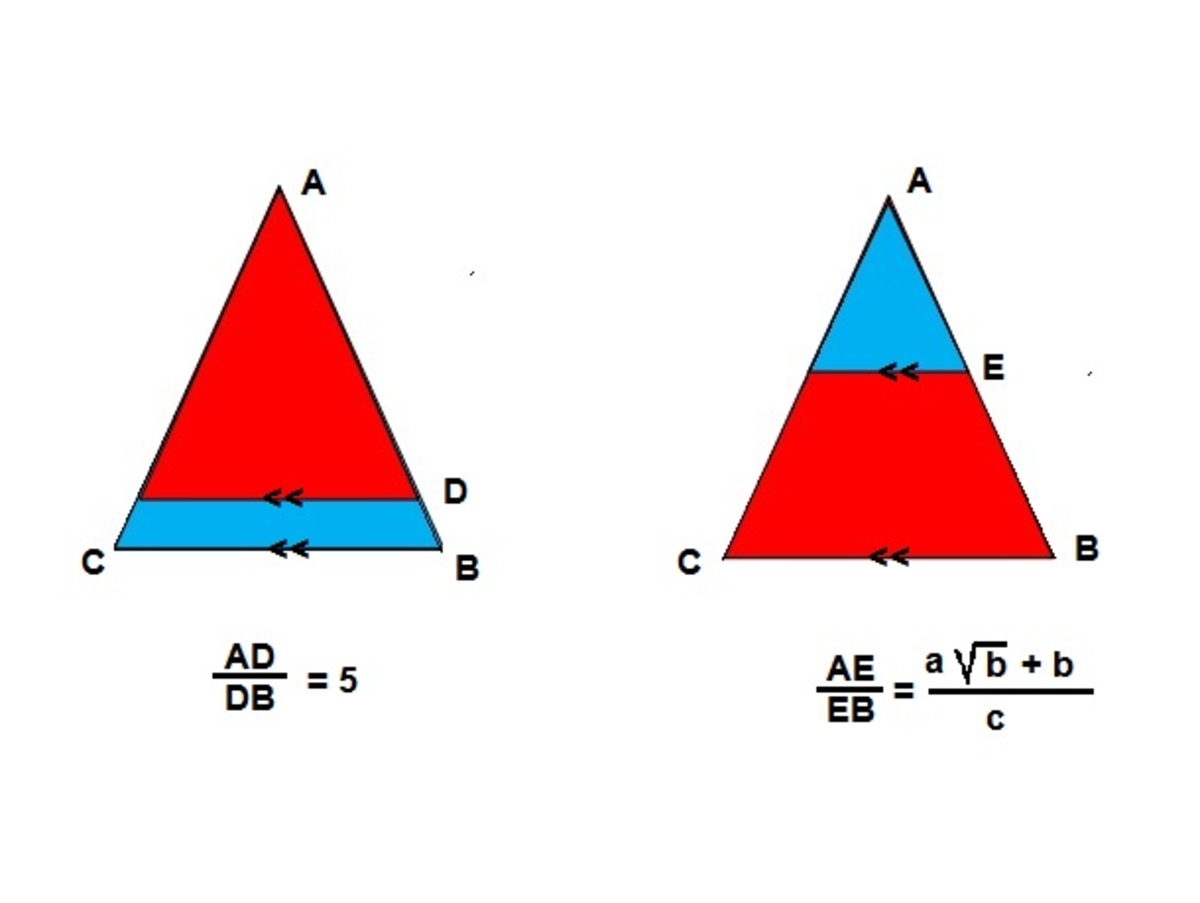
The answer is 42.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
From the left figure, the red triangle is similar to △ A B C . Therefore, the ratio of their areas A △ A r e d = ( A D + D B ) 2 A D 2 = ( 5 + 1 ) 2 5 2 = 3 6 2 5 . ⟹ A r e d = 3 6 2 5 A △ , ⟹ A b l u e = A △ − A r e d = 3 6 1 1 A △ .
From the right figure,
A △ A b l u e ⟹ ( A E + E B ) 2 A E 2 A E + E B A E E B A E + 1 E B A E ⟹ E B A E = 3 6 1 1 = 3 6 1 1 = 6 1 1 = 6 1 1 = 6 − 1 1 1 1 = ( 6 − 1 1 ) ( 6 + 1 1 ) 1 1 ( 6 + 1 1 ) = 2 5 6 1 1 + 1 1 Taking square root both sides Divide up and down of LHS by E B
Therefore, a + b + c = 6 + 1 1 + 2 5 = 4 2 .