Diving Paraboloid
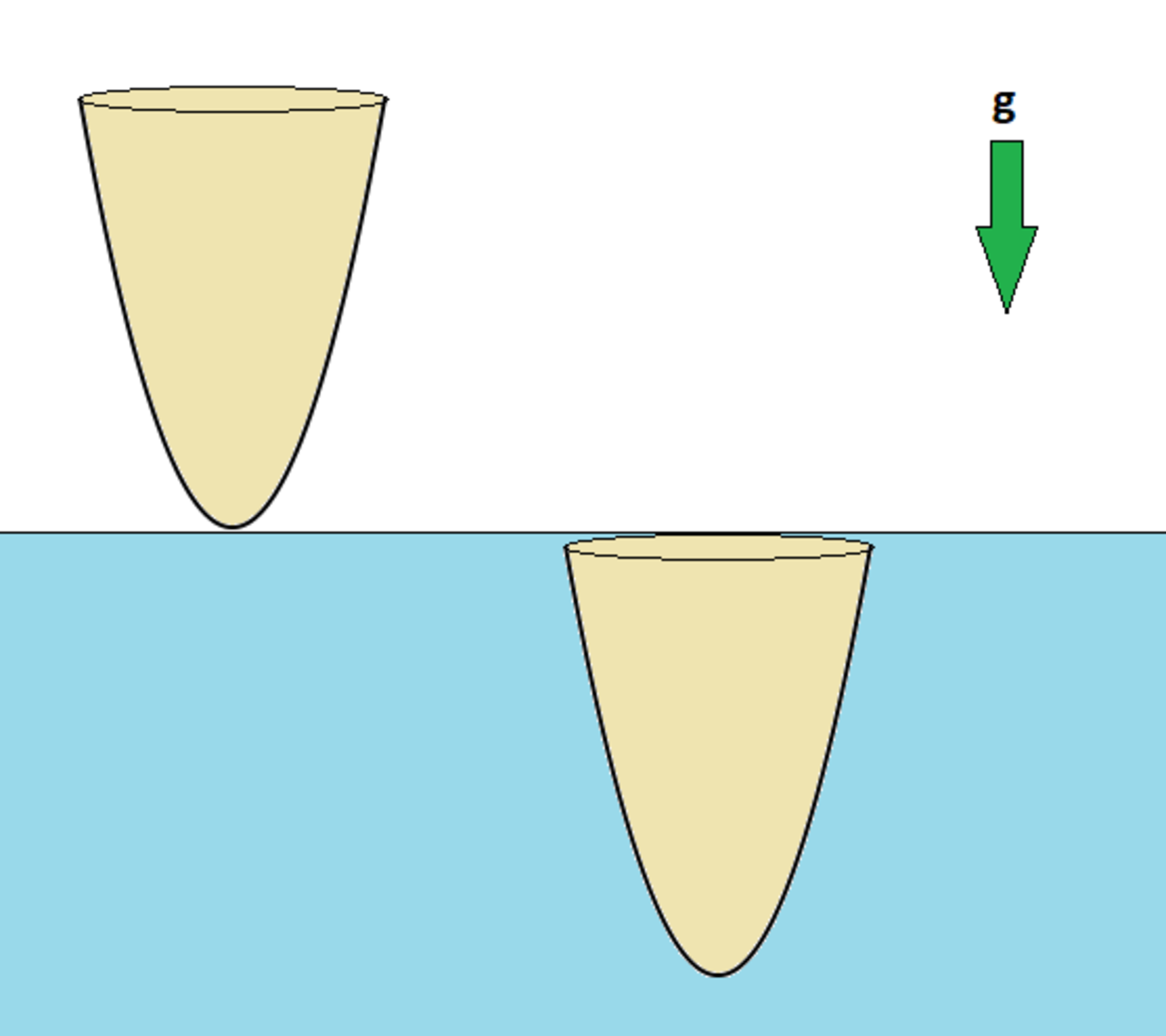
Consider a solid object of uniform mass density whose outer surface is a revolved parabola, and whose top is a flat circular disk. The object is initially upright and at rest, with its vertex touching the surface of a body of water.
The object falls into the water, and has zero speed at the instant it becomes fully submerged. What is the ratio of the density of the object to the density of the water (to 3 decimal places)?
Details and Assumptions:
- There is an ambient downward gravitational field.
- Assume that the buoyant force is the only force exerted by the water on the object.
The answer is 0.333.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let us call:
First, if we assume that the paraboloid follows the relation by a constant a :
H = a R 2
Then, also:
y = a x 2
Dividing both equations:
x 2 = H R 2 y
Writing the differential equation of the paraboloid, since its displaced volume is 2 π x 2 y :
m d t d v = m g − ρ H 2 O g 2 π x 2 y
d t d v = g − ρ H 2 O g 2 m H π R 2 y 2
Let us define:
k ≜ ρ H 2 O g 2 m H π R 2
d t d v = g − k y 2
d y d v d t d y = g − k y 2
d y d v v = g − k y 2
v d v = ( g − k y 2 ) d y
Since at y = 0 , v is also 0 (paraboloid begins at rest):
∫ 0 v v d v = ∫ 0 y ( g − k y 2 ) d y
2 v 2 = g y − 3 k y 3
At y = H (instant in which paraboloid is fully submerged), v is also equal to 0 :
0 = g H − 3 k H 3
H 2 = k 3 g
H 2 = 3 g π R 2 g ρ H 2 O 2 m H
2 π R 2 H 3 m = ρ H 2 O
3 ρ p a r = ρ H 2 O
ρ H 2 O ρ p a r = 3 1 = 0 . 3 3