Division of Square

Let the shorter length of the other intersecting side by $x$ . Then the area of the smaller part $A_s = \dfrac {x+\frac 12}2 \times 1 = \dfrac {2x+1}4$ and that of the bigger part $A_B = \dfrac {1-x+\frac 12}2\times 1 = \dfrac {3-2x}4$ . It is given that:

$\begin{aligned} \frac {A_B}{A_s} & = \frac 21 \\ \frac {3-2x}{2x+1} & = 2 \\ 3-2x & = 4x+2 \\ 6x & = 1 \\ \implies x & = \frac 16 \end{aligned}$

The length of the intercept:

$\begin{aligned} l & = \sqrt{\left(\frac 12 - x\right)^2 + 1^2} \\ & = \sqrt{\left(\frac 12 - \frac 16 \right)^2 + 1} \\ & = \frac {\sqrt{10}}3 \end{aligned}$

$\implies a+b = 10 + 3 = \boxed{13}$

Letting the side of the square be $1$ , we see that the cutting line cuts one of the sides of the square into two halves. As for the opposite side, it cuts the side into $x$ and $(1-x)$ . We first determine the value of $x$ as follows:

Considering that one part of the square is twice the area of the other, we have:

$\frac{x+\frac{1}{2}}{2}=2(\frac{1-x+\frac{1}{2}}{2})$

$x+\frac{1}{2}=2(1+\frac{1}{2}-x)$

$x+\frac{1}{2}=2+1-2x$

$x+\frac{1}{2}=3-2x$

$(1+2)x=3-\frac{1}{2}$

$3x=\frac{6-1}{2}$

$3x=\frac{5}{2}$

$x=\frac{5}{3\times2}$

$x=\frac{5}{6}$

Now we know one of the sides is divided into $\frac{5}{6}$ and $\frac{1}{6}$ . Employing Pythagoras' Theorem, the length of the line is $\sqrt{(\frac{1}{3})^2+1^2}=\sqrt{\frac{1}{9}+1}=\sqrt{\frac{1+9}{9}}=\sqrt{\frac{10}{9}}=\frac{\sqrt{10}}{3}$ .

Then $a+b=10+3=\boxed{13}$

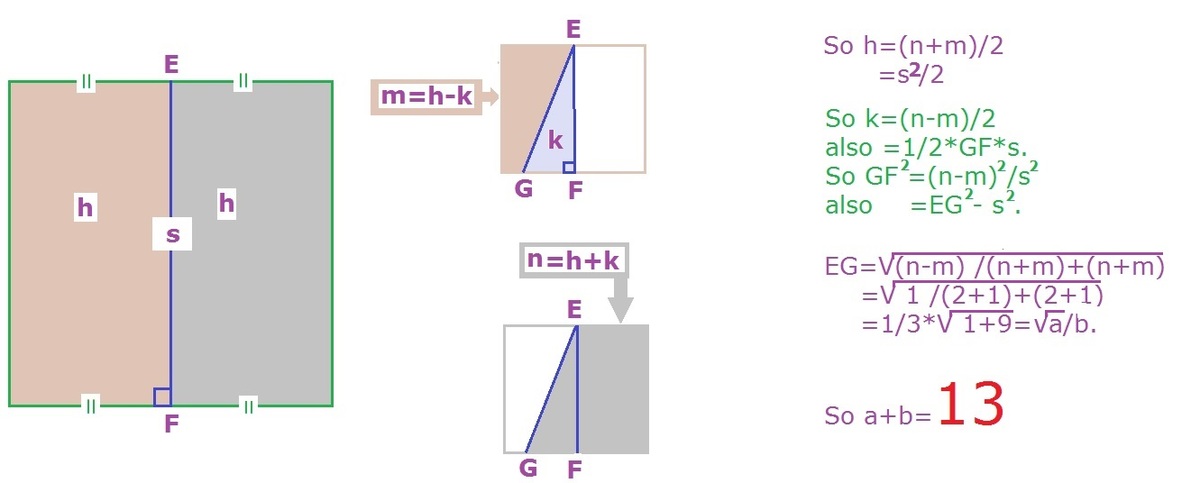
WLOG we first divide the square side 1, into half by joining midpoints of the a pair of opposite sides
say MN $\bot$ to side containing N.
If we add 1/6 th of the area to the right partition, and subtract from the left, we get,
1/2+1/6=2/3 on the right and 1/2-1/6=1/3 on the left , the ratio we require. Let P on the left of N on the same side of the square containing N, such that PN=1/3. So the area to the left of MP is 1/3 and that to the right is 2/3 and Area of rt. triangle MPN=1/6.
Since MN=1, and PN=1/3,
$Hy. MP= \sqrt{1^2+(1/3)^2}=\sqrt{10} /3=\sqrt a /b.$ .
a+b=13.