Dlanod is aiming higher
The sky is the limit: Mr. Dlanod, the notorious developer, in now planning a cluster of four space hotels orbiting Earth (or Moon or Mars...), such that any two of them stay at a distance of 1.8 km at all times. A network of tubes needs to be built so that any hotel is connected to any other (possibly including some junction points in space), but the budget allows for at most 4.4 km of tubes.
Can the task be accomplished?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Yes, that is exactly what I found. Thank you! I will post my solution to fill in some details.
Without the ambition of finding the Steiner minimal tree, we merely attempt to meet the budget constraint, using the 2D-case as a guide. Working with a distance of 2 km rather than 1.8 km at first, for convenience, we place our four hotels at ( ± 1 , 0 , 0 ) (the "lower hotels") and ( 0 , ± 1 , 2 ) ("the upper hotels") . Our intuition and our understanding of the 2D-case (see Figure 7 here ) suggest to introduce two symmetric junction points ( 0 , 0 , z ) and ( 0 , 0 , 2 − z ) , connect ( 0 , 0 , z ) to the two "lower" hotels, and connect ( 0 , 0 , 2 − z ) to the two "upper" hotels. The total length of the five tubes in this design turns out to be f ( z ) = 4 1 + z 2 + 2 − 2 z . It is a straightforward calculus exercise to show that the minimum of f ( z ) is 2 + 2 3 , attained when z = 3 1 . If the distance between the hotels is required to be 1.8 km rather than 2 km, then the corresponding network has a length of 0 . 9 ( 2 + 2 3 ) ≈ 4 . 3 9 km, meeting the budget constraint. Thus, Y e s , the task can be accomplished.
The attached graph is shifted down by 2 1 , for symmetry.
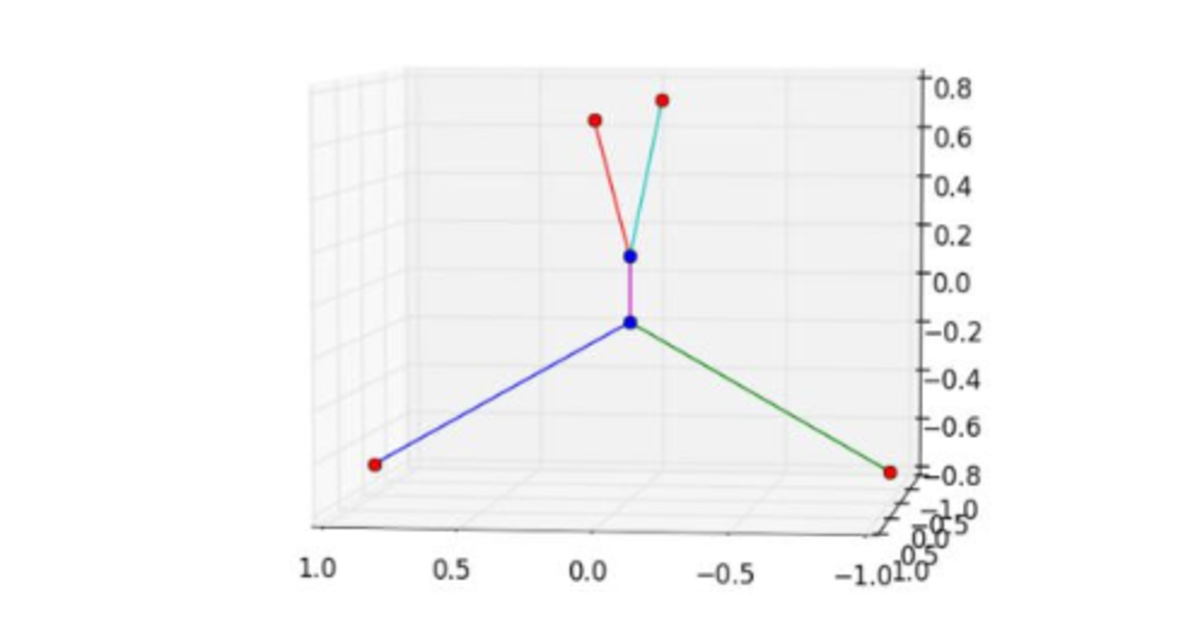
We want to find a Steiner minimal tree for the vertices of a regular tetrahedron of side length 1 . 8 km.
My intuition would be to create a Steiner minimal tree between two vertices and the centroid of the tetrahedron, and then reflect this tree through the centroid and rotate it through 9 0 ∘ to create a Steiner minimal tree between the other two vertices and the centroid.
This system can be shown to have length 1 . 8 ( 3 + 2 1 ) = 4 . 3 9 0 4 8 3 6 6 km, making Dlanod's task possible.