Dlanod is building huts, yet again
Dlanod the greedy developer is still dreaming of buying a square plot of land on a tropical island and building some vacation huts on in, circular as viewed from above, each with a diameter of six meters. He has not given up on his plan to build them wall-to-wall, although this might be a bit inconvenient for the unfortunate tourists who will have to stay there. Dlanod's chief architect, who went to Yale, advises him that, regardless of the details of the arrangement, he will have to buy at least 6 2 = 3 6 square meters of land for each hut. Dlanod states that "his intuition" tells him otherwise, and he will be able to do better. Who is right?
Arguing "from first principles," prove the architect's claim, or provide a detailed plan for an arrangement (including the number of huts and the size of the plot) that proves the architect wrong.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Yes, indeed! Thank you! Now, knowing your love of solutions "from first principles," I was asking for one. Can you provide one? As the architect points out, in his defense: You can't believe everything you find on the Internet.
To get around the building regs, Dlanod is now planning to build in the US possessions (colonies?), where (building) deregulation now reigns supreme.
Log in to reply
I've moved my first principles demonstration up into the main entry.
Yes, the proof from first principles works, thank you! Being a lazy guy myself, I will propose a solution that requires less computation and "moving things a little" if and when I find the time. (Incidentally, I'm packing my bags as I will spend the month of January in a little hut in the Caribbean; luckily, that development is not so densely packed). Meanwhile, I will propose one more problem in this Dlanod saga.
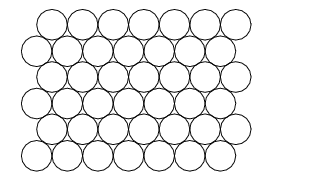
The plan is to place the huts in a "honeycomb pattern," in p rows with q cottages each, as shown in the attached figure, where p = 6 and q = 7 . We can place the huts onto a rectangular plot with length L = 6 q + 3 and width W = 6 + 3 3 ( p − 1 ) . For example, if we choose p = 9 and q = 7 , then L = 4 5 , and W < 4 7 . 6 , so that we can place these 63 huts on a square plot with side length 47.6 meters. The amount of land we need per cottage will be 6 3 4 7 . 6 2 < 3 6 square meters.
Once again, Dlanod is right .
What is 'from first principles' ?
This website gives a distressingly complete listing of circle-packing solutions. In particular, it shows how to pack 3 0 circles of radius 0 . 0 9 1 6 7 1 0 5 7 9 8 5 9 8 8 4 3 8 7 1 8 8 0 6 5 9 9 2 3 3 in a square of side 1 . This means that 3 0 huts of radius 3 metres can be packed inside a square of side 3 2 . 7 2 5 7 0 4 9 9 2 5 0 1 9 7 6 1 5 2 3 0 6 4 1 5 6 2 8 metres, which means we have 3 0 3 2 . 7 2 5 7 0 4 9 9 2 5 0 1 9 7 6 1 5 2 3 0 6 4 1 5 6 2 8 2 = 3 5 . 6 9 9 0 5 8 9 0 8 5 4 2 2 9 2 2 3 3 7 0 1 6 6 7 2 1 8 square metres per circle. This makes Dlanod right. Considering the other optimal packings given on that website, 3 0 huts is the smallest number for which less than 3 6 square metres per hut is possible.
Of course, Dlanod will need the assistance of his colleague Jerry Mandau to get around the building regs for this planned design.
Here is a theoretical justification, as well.
Start off by packing six columns of five 3 metre radius huts in a hexagonal array in a 3 3 × 3 3 metre square. I will show how to adjust this pattern to fit the huts in a 3 2 . 8 × 3 2 . 8 metre square, which gives 3 5 . 8 6 1 3 square meters per hut (not optimal, but enough to answer the question).
The initial array of huts fills the vertical height of the 3 3 × 3 3 square, and there is a strip of width 3 3 − ( 6 + 1 5 3 ) = 1 . 0 1 9 2 4 metres free on the right. If I slide the third column of huts 2 6 2 − 2 . 8 2 − 3 3 = 0 . 1 1 0 4 5 metres to the right, then the second column of huts can shift a little to the right and drop down 0 . 2 metres (the triangle A B C has been stretched horizontally so that C is now 2 . 8 metres above the line A B , instead of its initial 3 metres). Readjust the fifth and fourth columns similarly, and shift the sixth column to match the second and fourth. The 3 0 huts are now placed in a rectangle that is 6 + 8 1 1 = 3 2 . 5 3 3 meters wide and 3 2 . 8 metres high. Thus we can certainly place 3 0 huts in a 3 2 . 8 × 3 2 . 8 metre square, and we are done.
It seems possible that this stretching approach will give us the optimal packing. If we want to fit the huts into an x × x metre square, we will need to drop C down 3 − ( x − 3 0 ) metres, and so we need to shift B a distance of 2 3 6 − ( x − 3 0 ) 2 − 6 3 metres to the right. If doing this (and performing similar shifts to the other columns) results in the huts fitting exactly inside the x × x metre square, then we must have 5 3 6 − ( x − 3 0 ) 2 + 6 = x which solves to give x = 3 2 . 7 2 5 7 0 4 9 9 2 5 0 1 9 5 .