Dlanod is building huts
Dlanod the greedy developer is at it again: He has bought a square plot of land on a Caribbean island, 3 6 × 3 6 meters, and he is planning to build some vacation huts on the plot, circular as viewed from above, each with a diameter of 6 meters. Initially he is planning to build 3 6 huts, wall to wall, but local regulations require a distance of more than 1 2 meters between the huts. He is allowed to build right up to the boundary of the plot, though. What is the maximal number of huts Dlanod can build under these constraints?
Bonus: Since Dlanod isn't comfortable with fractions, let alone irrational numbers, can you place the huts in such a way that their distances from the plot's boundary are all integers if measured in meters?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Yes, exactly! Nice graphic! Thank you! When I constructed the problem, I came up with essentially the the same integer configuration, ( 1 3 , 3 ) , ( 3 3 , 3 ) , ( 3 , 1 8 ) , ( 2 3 , 1 8 ) , ( 1 3 , 3 3 ) , ( 3 3 , 3 3 ) , placing the origin at the lower left corner.
But finding these six points is the easier part: How can we convince our friend Dlanod that he cannot build 7, 8, or 100 huts? ;)
Log in to reply
Subdivide the central 3 0 × 3 0 square (the target square for the centres of the huts) into six 1 5 × 1 0 rectangles.
If Dlanod could place seven huts on the plot, at least one of these rectangles would contain two hut-centres, courtesy of the pigeonhole principle. Since the length of the diagonal of one of these rectangles is 5 1 3 = 1 8 . 0 2 7 8 m, this means that the two hut-centres must each be "close" to (i.e. within a centimetre or so of) a diagonally opposite pair of vertices for that rectangle. No rectangle can contain more than two hut-centres.
If any rectangle contains a hut-centre "close" to a rectangle vertex v , then any other rectangle that shares that same vertex can only contain at most one hut-centre, which will be "close" to the vertex diagonally opposite to v .
Suppose that two of the six rectangles contain two hut-centres. Either: (a) these two rectangles possess hut-centres that are "close" to four vertices of the same colour (either red or green in the diagram), in which case it is clear (on considering cases) that it is only possible to choose at most one additional hut-centre for each additional remaining vertex of the same colour, or (b) hut-centres have been chosen "close" to the vertices 2 , 5 , 8 , 1 1 (or a similar configuration), in which case it is clear that no further hut-centres can be chosen. Thus it is not possible to choose seven hut-centres in this case.
Thus we must have one rectangle containing two hut-centres, with the other five rectangles containing one hut-centre each. If the rectangle containing two hut-centres does not contain a hut-centre "close" to either vertex 6 or vertex 7 , then this rectangle must contain hut-centres "close" to vertices 2 and 5 (or similar - vertex pairs ( 5 , 1 0 ) , ( 3 , 8 ) and ( 8 , 1 1 ) are also possible). But then the upper middle rectangle will contain a hut-centre "close" to vertex 7 . Thus there must be a hut centre close to one of vertices 6 and 7 . For definiteness, suppose that we have a hut-centre close to vertex 6 .
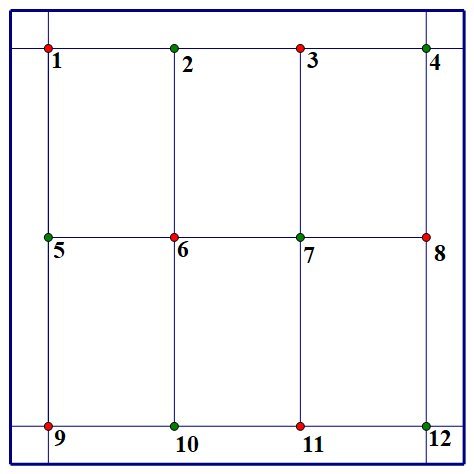
If the rectangle containing two hut-centres contains vertex 6 , then we must have five hut-centres in the left-hand four rectangles, and these must be "close" to the vertices 1 , 3 , 6 , 9 , 1 1 . But then it is impossible to find one more hut-centre in each of the remaining two rectangles, since any further hut-centre must be "close" to vertex 8 . If the rectangle containing two hut-centres does not contain vertex 6 , then there will be four hut-centres in the left-hand four rectangles, one "close" to vertex 6 and the other three "close" to three of the vertices 1 , 3 , 9 , 1 1 . Thus there will be a hut-centre "close" to at least one of the vertices 3 , 1 1 . If we have chosen hut-centres "close" to both of vertices 3 , 1 1 , then neither of the remaining rectangles can contain two hut-centres. If we have chosen a hut-centre "close" to vertex 3 only, then the bottom-right rectangle must be the one to contain two hut-centres, which will be close to vertices 8 , 1 1 , in which case the upper right rectangle cannot contain a hut-centre. We obtain a similar contradiction if we have chosen a hut-centre "close" to vertex 1 1 only. Thus it is not possible to choose seven hut-centres.
This proves that 6 is the greatest number of possible hut-centres.
Mark Hennings has written a careful solution showing how we can build six huts on the plot. To summarize: We can place the centers of the huts at the points ( 1 3 , 3 ) , ( 3 3 , 3 ) , ( 3 , 1 8 ) , ( 2 3 , 1 8 ) , ( 1 3 , 3 3 ) , ( 3 3 , 3 3 ) , with the origin in the lower left corner. Any two of these points will be at least 3 2 5 > 1 8 meters apart, which implies that the distance between the huts will be more than 12 meters as required.
But there is more work to be done: We need to convince Mr Dlanod that he will not be able to build seven huts (or more) to these specifications. Rather than proving this fact from first principles, which is quite tedious, we will relate this problem to another, better understood question that turns out to be equivalent: Can we fit seven non-overlapping circles of radius 9 into a 4 8 × 4 8 meter square (we are moving each side of the plot out by 6 meters). Indeed, if we have a solution to the original problem, then we can solve the new problem by enlarging the radius of all the huts from 3 to 9, and vice versa.
The problem of whether one can fit n non-overlapping circles of radius r into a square with side-length a has long been studied and is well understood, at least for small values of n . In particular, it turns out that seven circles can be packed into the square if r a ≥ 4 + 3 . In our case we have r a = 9 4 8 < 4 + 3 , so that it is impossible to pack 7 circles of radius 9 into a square with side-length 48.
Thus the largest number of huts that can be built is 6 .
First principles proof provided. The basic principle is clear, but a little fiddling is required to make it work
Going with the circle-packing argument, this page tells us that seven circles of radius r can be packed in a unit square provided that r ≤ 1 3 1 ( 4 − 3 ) . Thus the maximum radius in a square of side 4 8 is 1 3 4 8 ( 4 − 3 ) = 8 . 3 7 4 . Thus we cannot pack seven circles of radius 9 in a square of side 4 8 .
Of course, the original proof about the circle-packing was probably even more detailed than my "first principles" proof...
The best that can be done is 6 huts.
Put points A and E into corners of the plot, 3 m away from the plot edges. Then place point C a distance of 1 8 m from both A and E . Extend the lines A C and E C to place huts B and F so that A B F E is a rectangle with C at its centre. Then create triangle B D F congruent to A C E . Note that A B = C D = E F = 6 1 1 > 1 8 , while 9 1 1 = 2 9 . 8 4 9 6 < 3 0 , and so there is just room to build huts with centres at A , B , C , D , E , F .
This set-up has some huts exactly 1 2 m from each other. However, Dlanod has some 1 6 cm of slack in the the placement of point D , and so he could ease this construction slightly, perhaps constructing point C at distance of 1 8 . 0 2 m from A and E , and satisfy the building regs. Or else see below!
For integral distances to the boundary, keep A and E where they are. Move B and F a little to the right, so that A B = E F = 2 0 m (the previous value of A B was 6 1 1 = 1 9 . 8 9 9 7 m). Place D midway down the right-hand side, a distance 3 m from the edge, and have C on the same level, with C D = 2 0 m. Then A , B , D , E , F are all 3 m from the boundary, while C is 1 3 m from the boundary. Also A C = B C = E C = F C = 5 1 3 = 1 8 . 0 2 7 8 m