Dlanod's Adventures, continued

Geometry Level 3

Due to budgetary and regulatory obstacles, the notorious developer, Mr. Dlanod, is forced to scale down his plans: He is now planning to build six hotels in the wilderness (complete with casinos and golf courses), at the points ( x , y ) (x,y) with x = 0 , 2 , 4 x=0,2,4 and y = 0 , 2 y=0,2 where distances are measured in kilometers. A network of roads needs to be built so that any hotel is connected to any other, but the budget now allows for at most 9.4 km of roads.

Can the task be accomplished?

This is a sequel to this problem .

Yes No An open problem

Otto Bretscher by Otto Bretscher , 65, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Mark Hennings
Nov 14, 2018

Connect a Steiner system for the left-hand quartet of hotels with a Steiner system for an isosceles right-angled triangle of hotels formed by the remaining two hotels and one of the two central hotels.

The total length of this system is 6 + 2 + 2 3 + 2 = 9.3278 \sqrt{6} + \sqrt{2} + 2\sqrt{3} + 2 = 9.3278 km.

7 Helpful 0 Interesting 0 Brilliant 0 Confused

Yes, that works.

My intuition tells me that you could do slightly better by finding the optimal Steiner tree for (0,0), (0,2), (2,2), and (2,1) and then reflect it across (2,1), but I have neither the patience nor the time to find that tree exactly (quite a tedious and dreadful task, as you know). Some numerical experimentation led me to the approximate Steiner points (0.55,1.2) and (1.75, 1.3), with their reflections in the "right-hand quartet of hotels," as you put it. I believe the total length of the roads comes out to slightly less than 9.3 km (around 9.25), but I played it safe in the wording of my problem and allowed 9.4, which permits your intriguing design that is very easy to compute.

Otto Bretscher - 2 years, 6 months ago

Log in to reply

Not too hard, given a geometry drawing package. Take care to construct the right Steiner system for ( 0 , 0 ) (0,0) , ( 0 , 2 ) (0,2) , ( 2 , 0 ) (2,0) (not ( 2 , 2 ) (2,2) ) and ( 2 , 1 ) (2,1) , since there are two. Both of them fit an irregular, but 12 0 ∘ 120^\circ , hexagonal mesh onto the six points.

The left-hand one has length 9.25036 9.25036 km, while the right-hand one is much longer, with length 10.07816 10.07816 km. It is not hard to evaluate the smaller length explicitly, since the left and right sides of the quadrilateral of vertices are parallel. This network has length 2 11 + 6 3 2\sqrt{11+6\sqrt{3}} . We can also calculate the second Steiner network to have length 2 15 + 6 3 2\sqrt{15+6\sqrt{3}} .

Mark Hennings - 2 years, 6 months ago

Log in to reply

Of course these computations are not hard, but, by my impatient standards, they are tedious. For a practical problem like this, I'm content with a good numerical approximation.

Yes, the one on the left is what I had in mind (reflected over y = 1 y=1 ). It looks like it might be the optimal Steiner tree.

Otto Bretscher - 2 years, 6 months ago

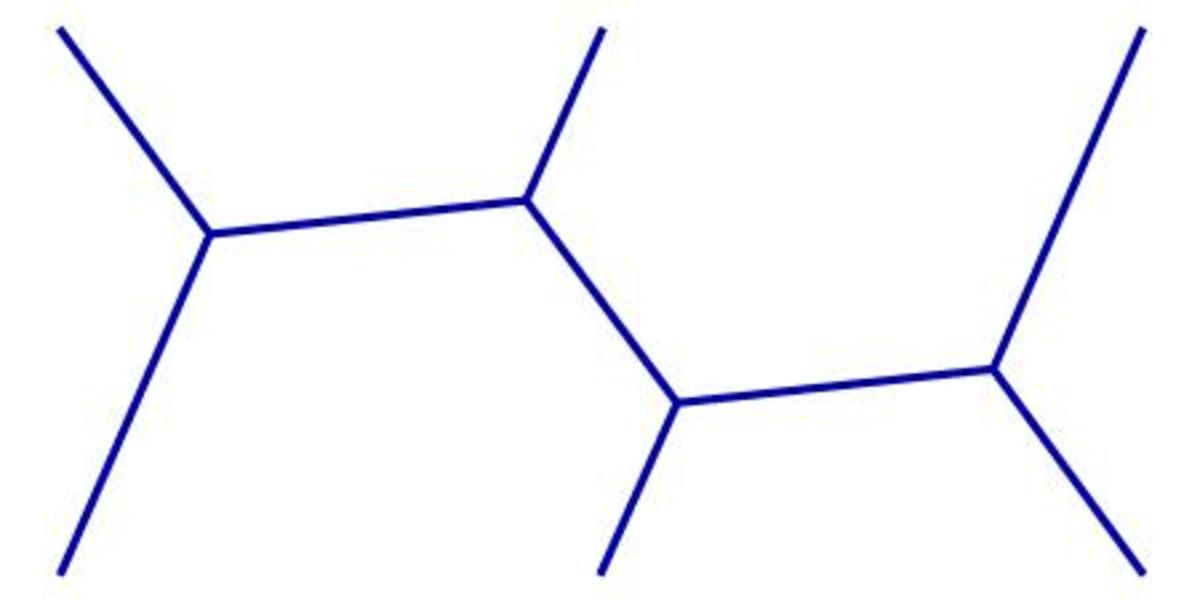
Doing it this way gets a total road length of something like 9.25...just a rough approximation

4 Helpful 0 Interesting 0 Brilliant 0 Confused

Yes, exactly. These seem just about the Steiner points I found, (0.55,1.2) and (1.75, 1.3), also by making a rough approximation, which will suffice in a practical problem like this. This is indeed the best we can do, referred to as the "optimal Steiner tree."

Otto Bretscher - 2 years, 6 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...