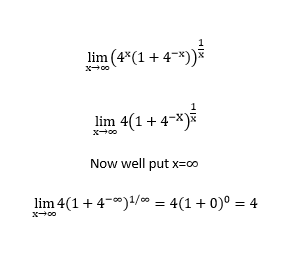Dominating Matter
 x
→
∞
lim
(
4
x
+
1
)
x
1
=
?
x
→
∞
lim
(
4
x
+
1
)
x
1
=
?
Try to solve this without using L'hopital Rule.
Image Credit: Flickr Hans Proppe .
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
x → ∞ lim ( 4 x + 1 ) x 1 = e l i m x → ∞ x 1 ⋅ l n ( 4 x + 1 ) = e l i m x → ∞ x 1 ⋅ l n ( 4 x ) = = e l i m x → ∞ x x ⋅ l n 4 = e l n 4 = 4
As x gets large, 4 x ≈ 4 x + 1 when you compare their magnitude. Since the inverse power primarily deals with the property of magnitude, the limit approximates to be ( 4 x ) x 1 which is equal to 4.
not exact i'll put the solution through few days
Log in to reply
I know it isn't. It's the way I thought of doing it though.
the correct solution without use L'hopital Rule.