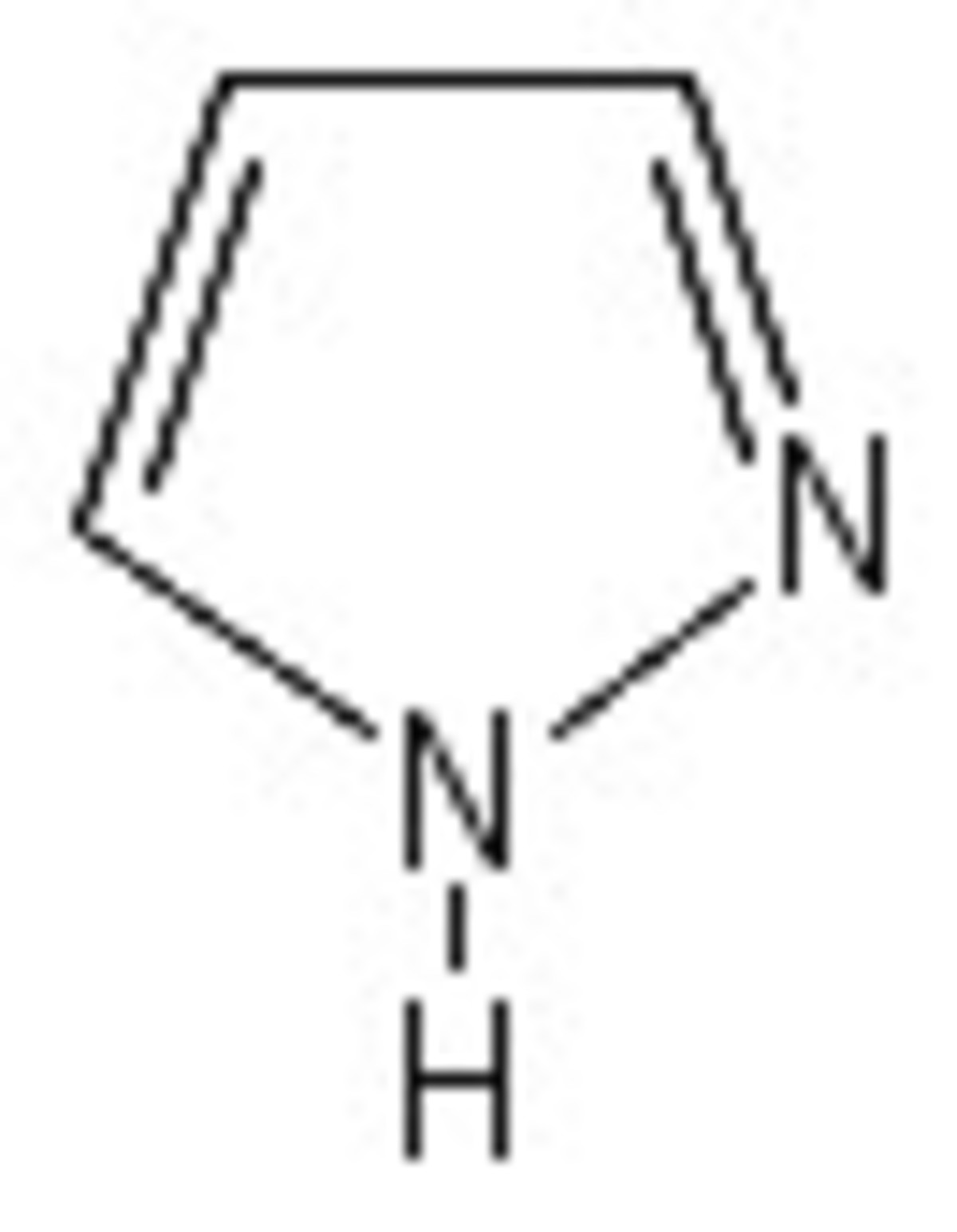
Do Golem breathe?

"I have seen a medicine, that's able to breathe life into stone . . ." .

(Image from DeviantArt)

In 2011, Russian researchers investigated a compound that appears to have tasted the medicine that Lafew describes in Shakespeare's play All's Well That Ends Well .

Consider a compound B of d-metal A whose chemical formula is $CsACl_{n}$ . When 0.948356g of this substance reacts with 0.23787g of $CsF$ and an excess of fluorine gas, it is observed that 1.388106416g of a red solid C is formed and 0.3334g of chlorine gas is evolved.

A forms a chelate complex with two moles of an organic compound D which is a symmetric diketone whose formula is $C_{5}H_{2}O_{2}F_{6}$ . This complex is dissolved in toluene and mixed with another organic compound W to form a large solvate complex Q . The process of producing W from precursor $\mu$ (shown below) proved to be inefficient.

To overcome this, the following sequence was introduced. We start with a compound T that is an acetal whose H-NMR contains 4 distinct signals and its intensities are in the ratio 1:1:4:6.

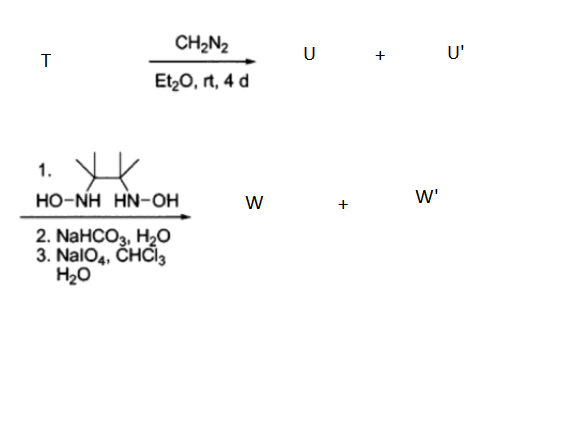
W is radical species of the formula $C_{10}H_{15}N_{4}O_{2}$ .

The final product mix contains regio-isomers that can be easily separated. We distinguish the isomers using a H-NMR machine that can detect coupling no greater than 3J values. W observes coupling at regions greater than 7.9 ppm, while W' observes coupling in the 5.9 - 7.2 ppm range.

The solvate complex forms many different crystals, one of these crystals contain a long chain of repeating units and we call this unit G . G can be considered to be an octahedral complex and at a transition temperature of 150K it changes from a trans form to a pseudo-cis form in a reversible manner without disturbing the integrity of the chain.

Let n denote the number of pseudo-cis units, it is given by the following statistical equation :

$n = 10^{70}exp(\frac{-4637}{150-T})$ for all temperatures T less than 150K

When many units G morph into the pseudo-cis configuration the crystal shrinks in volume. The ratio of volume at T and the volume at 150K be governed by the empirical formula :

$\frac{V_{T}}{V_{150}} = (1-\frac{n}{10^{5}})$

We now define certain quantities:

$\alpha$ is the number of rings in W

$\beta$ is the valency of A in compound C

$\gamma$ is the ratio between volumes at T = 120K (taken up to two decimal places)

Calculate the value of $\alpha + \beta +100\gamma$

Bonus:

• Deduce the formula of compounds A - C
• Deduce the structure of compounds T - W
• Deduce the structure of G in trans configuration
• If T is varied periodically, what motion does the crystal mimic?