Do I need calculus?

Geometry Level 1

Two sides of a triangle are 5 and 6. Find the maximum possible area of the triangle and round it off to nearest integer.

17 15 18 11 16 20 14 19

View wiki
Archit Boobna by Archit Boobna , 20, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Parth Bhardwaj
Apr 16, 2015

Area of a triangle can be expressed as - [absin(x)]/2 {half of the product of the sides and the sine of angle between them} . So in this case a=5 and b=6, which are constant, only the angle between them can change thus area of the triangle would be maximum for maximum value of sinx , which is = 1. So the area woul be equal to (5)(6)/2 which is equal to 15 !!!

4 Helpful 0 Interesting 0 Brilliant 0 Confused

Use latex please

Archit Boobna - 6 years, 1 month ago

Log in to reply

A r ( Δ ) = 1 2 a b sin ⁡ θ = 15 sin ⁡ θ ( A r ( Δ ) ) m a x = 15 { a t θ = 90 o } \displaystyle{Ar(\Delta )=\cfrac { 1 }{ 2 } ab\sin { \theta } =15\sin { \theta } \\ { \left( Ar(\Delta ) \right) }_{ max }=15\quad \left\{ at\quad \theta ={ 90 }^{ o } \right\} }

Karan Shekhawat - 6 years, 1 month ago

Log in to reply

Thanks for the help

Archit Boobna - 6 years, 1 month ago
Ken Jan
Apr 24, 2015

I just used 5 and 6 as the Base and the Height in 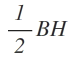still got the right answer but could someone explain... I don't really get me sometimes

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Area of any triangle can be given as 1 2 a b sin ⁡ C \frac 12 ab \sin C . Because ∣ sin ⁡ x ∣ ≤ 1 |\sin x | \leq 1 . The maximum area occurs when sin ⁡ x = 1 \sin x = 1 which means the angle C C is a right angle, so you're left with 1 2 a b \frac 12 ab .

Pi Han Goh - 6 years, 1 month ago

I did the same thing haha.

Christian Relleve - 5 years, 11 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...