Do it logically, or otherwise
Geometry
Level
4
Find the given angle @ .
It is in form A(degree) B (minutes). Find A + B.Note- It is the angle between the two given body diagonals.
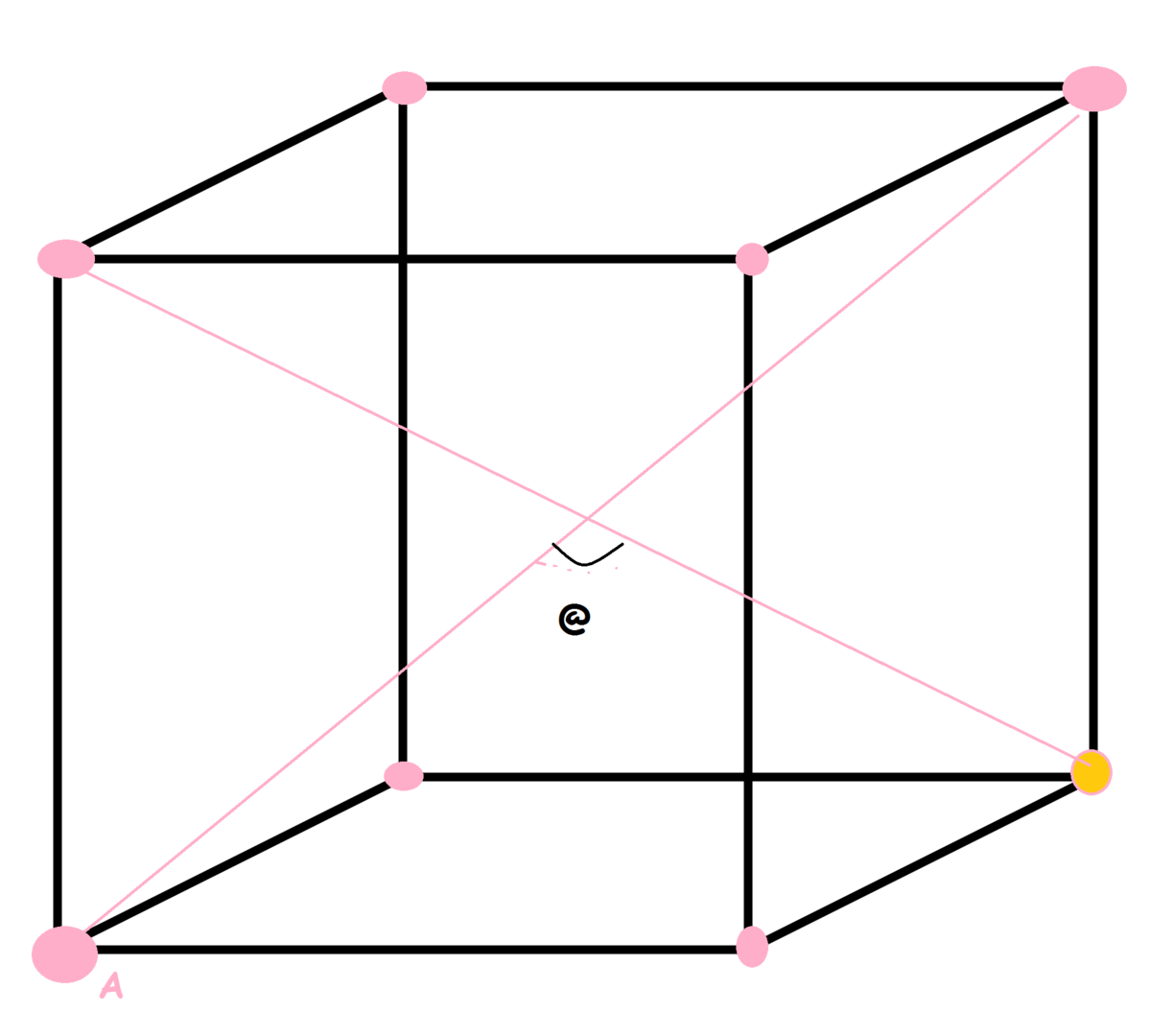
The answer is 137.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Image from https://app.geogebra.org/#geometry.
Let the cube have side length x. (I assume it is a cube)
The image above is a cross-section of the plane containing the diagonals.
It is a rectangle with sides x and 2 x .
By Pythagorean Theorem, the half-diagonal has length 2 3 x .
By cosine rule, ( 2 x ) 2 = 2 ( 2 3 x ) 2 ( 1 − cos @ ) 2 x 2 = 2 3 x 2 ( 1 − \cos@ ) 3 4 = 1 − \cos@ @ = arccos ( − 3 1 )
This is approximately equal to 1 0 9 degrees and 2 8 minutes. The final answer is A + B = 1 0 9 + 2 8 = 1 3 7