Don't Exceed but Evaluate

First lets use the identity ${ n }^{ -{ n }^{ 2 } }={ \left( { n }^{ -n } \right) }^{ n }$ then, $\lim _{ n\rightarrow \infty }{ { \left( { n }^{ -n }\left( n+1 \right) \left( n+\frac { 1 }{ 2 } \right) \left( n+\frac { 1 }{ 4 } \right) ...\left( n+\frac { 1 }{ { 2 }^{ n-1 } } \right) \right) }^{ n } } \\ =\lim _{ n\rightarrow \infty }{ { \left( \left( 1+\frac { 1 }{ n } \right) \left( 1+\frac { 1 }{ 2n } \right) \left( 1+\frac { 1 }{ 4n } \right) ...\left( 1+\frac { 1 }{ { 2 }^{ n-1 }n } \right) \right) }^{ n } } \\ =\lim _{ n\rightarrow \infty }{ { \left( 1+\frac { 1 }{ n } \right) }^{ n } } \times \lim _{ n\rightarrow \infty }{ { \left( 1+\frac { 1 }{ 2n } \right) }^{ n } } \times \lim _{ n\rightarrow \infty }{ { \left( 1+\frac { 1 }{ 4n } \right) }^{ n } } \times ...$

What is $\lim _{ n\rightarrow \infty }{ { \left( 1+\frac { 1 }{ an } \right) }^{ n } }$ ?

Simple, $\lim _{ n\rightarrow \infty }{ { \left( 1+\frac { 1 }{ an } \right) }^{ n } } \\ =\lim _{ n\rightarrow \infty }{ { e }^{ n\ln { \left( 1+\frac { 1 }{ an } \right) } } } \\ =\lim _{ n\rightarrow \infty }{ { e }^{ \frac { \ln { \left( 1+\frac { 1 }{ an } \right) } }{ \frac { 1 }{ n } } } } \\ =\lim _{ n\rightarrow \infty }{ { e }^{ \frac { \frac { 1 }{ a } \left( -\frac { 1 }{ { n }^{ 2 } } \right) \ln { \left( 1+\frac { 1 }{ an } \right) } }{ -\frac { 1 }{ { n }^{ 2 } } } } } \\ =\lim _{ n\rightarrow \infty }{ { e }^{ \frac { 1 }{ a } \ln { \left( 1+\frac { 1 }{ an } \right) } } } \\ ={ e }^{ \frac { 1 }{ a } }$

So, ${ e }^{ 1 }{ e }^{ \frac { 1 }{ 2 } }{ e }^{ \frac { 1 }{ 4 } }...\\ ={ e }^{ 1+\frac { 1 }{ 2 } +\frac { 1 }{ 4 } +... }\\ ={ e }^{ 2 }$

and ${ e }^{ 2 }$ is 7.389... so the answer is 7390.

We can rewrite the limit as $\exp \lim_{n\to \infty} n \sum_{k=1}^{n-1} \ln\left(1+\frac{1}{n2^k} \right).$ Use $\ln(1+x)=x+o(x)$ (Taylor series around zero), to get
$n \sum_{k=1}^{n-1} \ln\left(1+\frac{1}{n2^k} \right) =\left( \sum_{k=1}^{n-1}\frac{1}{2^k} \right)+o(1)$ Then the limit is $e^2$ .

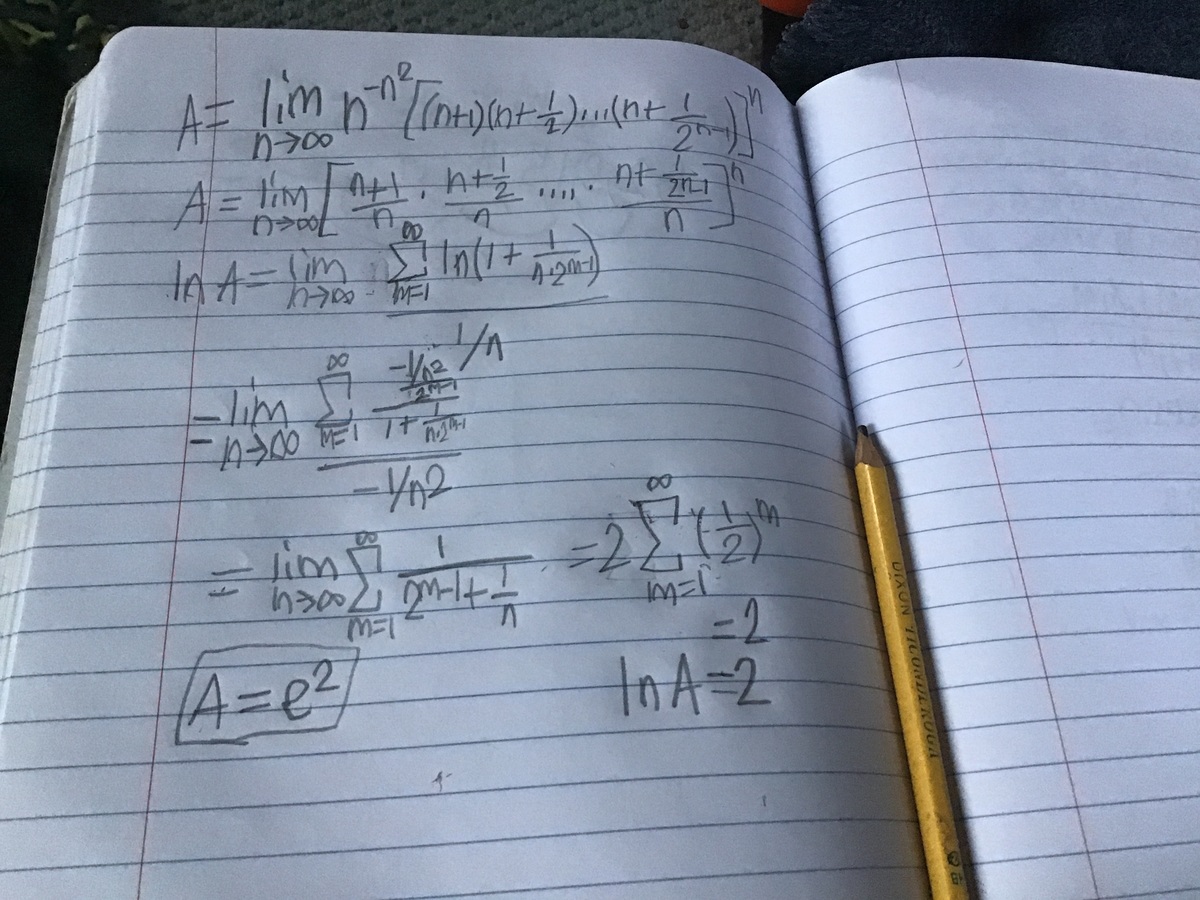I used L'Hopital's rule in step 4, and cancelled -1/n^2 in step 5. floor(1000 * e^2) = 7389