Do Not Use a Calculator: Divisibility By 13

Number Theory Level 1

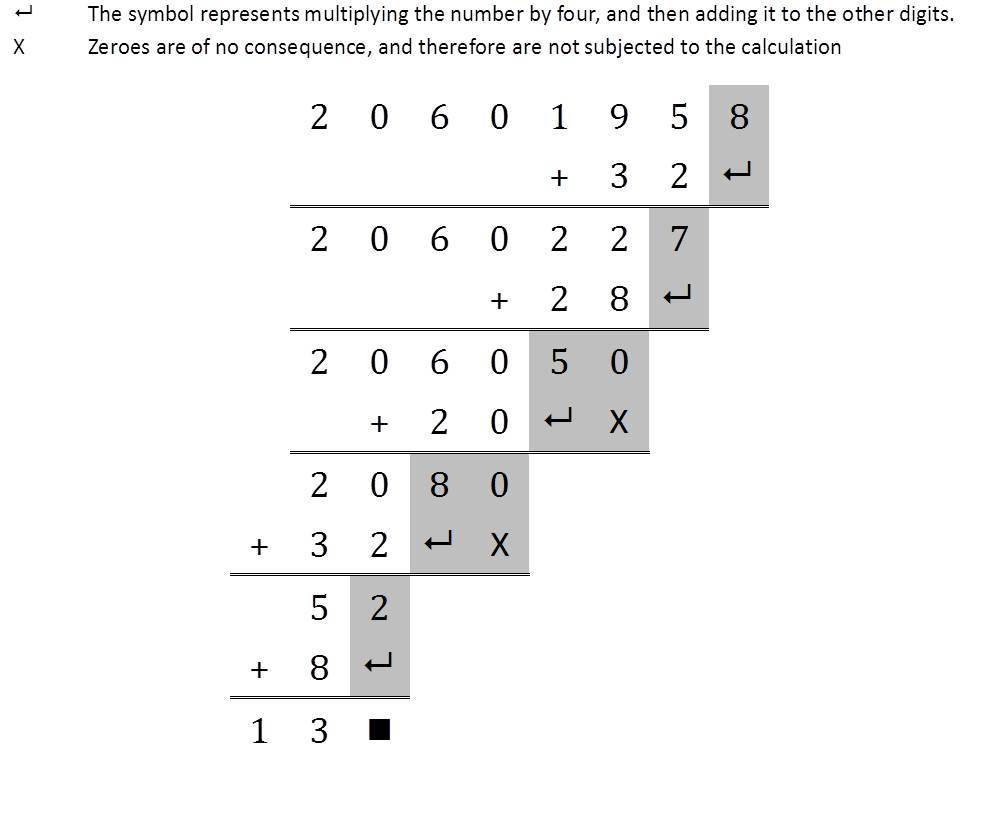
Is $20601958$ divisible by 13?

Can't Say Yes I Don't Know No

4 solutions

Parveen Soni
Oct 19, 2014

Add four times the last digit to the remaining leading truncated number. If the result is divisible by 13, then so was the first number. Apply this rule over and over again as necessary. (generally end when number become less than 130) like:- 2060195+8x4=2060227 and 206022+7x4=206050 and 20605+0x4=20605 and 2060+5x4=2080 and 208+0x4=208 and 20+8x4=52 and 52/13=4 hence given number is divisible

thank u :)

Maitri Mishra - 6 years, 5 months ago

Delano Might
Oct 28, 2015

Here utilizing the rule of 13s.

Ashtag Gaming
May 2, 2015

We can't use the calculator but we can still use the scratchpad!

Durrath Annes
Oct 17, 2014

I divided it by mind.. Please, tell me the short cut method to solve it...

Multiply each digit starting from right to left with the numbers.. $1,~10,~9,~12,~3,~4$ , in cycle, i.e.

Like this... The NO. $20601958$ What We Do : $8 \times 1 + 5 \times 10 + 9 \times 9 + 1 \times 12 + 0 \times 3 + 6 \times 4 + 0 \times 1 + 2 \times 10 = 195$ We see, 195 is divisible by 13 hence the result.

Also for last no. we got if it leaves a remainder 9 then also it is divisible by 13.

Arya :)

Arya Samanta - 6 years, 7 months ago

I didn't got the second step i.e 8 x 1+... . Please explain in more detail..

Parag Zode - 6 years, 7 months ago

check out by method

Parveen Soni - 6 years, 7 months ago

check out by method

Parveen Soni - 6 years, 7 months ago

Yep, I did the same thing. Didn't know the divisibility test for 13.

Joshua Lowrance - 2 years, 9 months ago

Do Not Use a Calculator: Divisibility By 13

4 solutions

0 pending reports