Do these hexagons count?
Does there exist an equiangular (interior angles are equal) hexagon with side lengths 1 , 2 , 3 , 4 , 5 , and 6 ?
If yes, is there more than one distinct way (up to rotation and reflection)?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Actually, the easier representation of a necessary and sufficient condition for an equiangular hexagon is that the sides (up to toggling lengths in each pair) satisfy
S = ∣ a − d ∣ = ∣ b − e ∣ = ∣ c − f ∣
Do you see why?
Hint: Think about what happens when we look at ( a − 1 , b , c , d − 1 , e , f ) . Also, there's a nice complex numbers representation of this fact.
In this case, the two hexagons satisfy S = 1 , 3 .
Log in to reply
Thank you! I was not aware of that identity, but I can see why it has to be so. When I have a chance, I'll try to edit my solution and simplify it along the lines you suggest. I came upon these shapes while I was thinking about the upside-down triangles problem.
I see the gist of the argument here, but what is the nice representation in complex numbers?
Log in to reply
Hint: For real numbers a , b , c , we have a + b ω + c ω 2 = 0 if and only if a = b = c .
This is a "well-known" fact about the cube roots of unity (which also has a similar pictorial proof). The reason why I like this explanation is that it helps us extend the argument to larger polygons. For example, the 30-gon case gets really really interesting, and the complexity is expressed by the analogous statement.
FYI I simplified your problem. Talking about equiangular but not equilateral triangles and quadrilaterals felt out of place because we were specifying the exact side lengths, so technically there is no equiangular quadrilateral with side lengths 1, 2, 3, and 4.
If the crux of the problem was "Does there exist an equiangular but not equilateral hexagon", then I think explaining the triangle and quadrilateral case would be helpful. Could you post that version, and maybe throw in the pentagon case too?
Log in to reply
Sure! It may take me a couple days, because of work, but that sounds fun.
Let's suppose that it is possible and that the hexagon has edges of lengths a , b , c , d , e , f going around clockwise. If we extend the edges of lengths a , c , e so that they meet we get an equilateral triangle. Ne notice that this triangle is also obtained by gluing equilateral triangles to the edges of lengths b , c , d . By calculating the length of the edges of the large equilateral triangle we get, a + b + c = c + d + e = e + f + a .
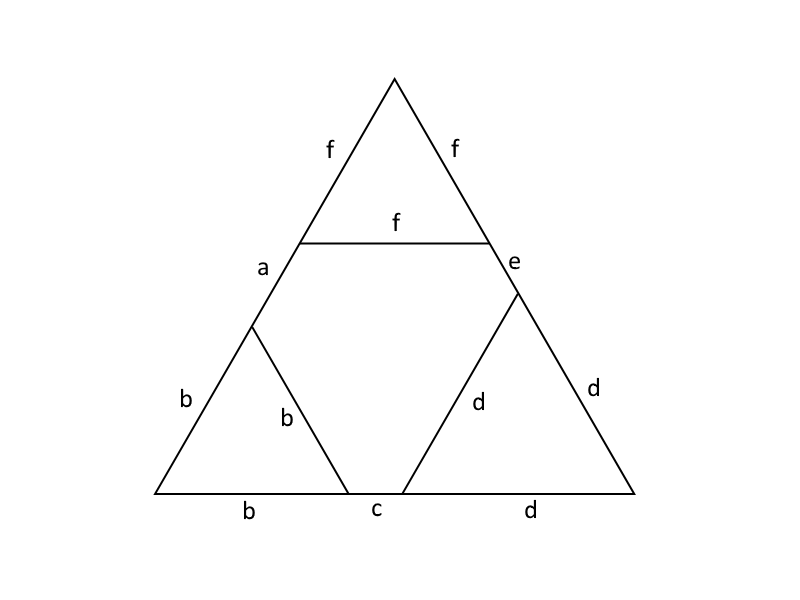
We can do the above starting by extending the other edges and we get, f + a + b = b + c + d = d + e + f . In fact any sequence satisfying these two equations is a solution to the problem. By subtracting these two sets of equalities from each other we get, c − f = e − b = a − d , this means that the difference between edge lengths of opposite faces is the same. Now there's only a few cases to check.
If 1 is opposite 2 then the difference is 1 and so 3 must be opposite 4 and 5 opposite 6 . This gives the solution 1 , 6 , 3 , 2 , 5 , 4
If 1 is opposite 3 then the difference is 2 but then 5 cannot be opposite any number we have to choose.
If 1 is opposite 4 then the difference is 3 and this gives a solution 1 , 6 , 2 , 4 , 3 , 5 .
It can also be checked that 1 cannot be opposite 5 or 6 . So there are exactly 2 different ways to form the required hexagon.
Nice observation.
Actually, the 2 equations that you started off with are equvalent - if you take ( a + b + c + d + e + f ) and subtract off the first equation, then we get the second equation (suitably reordered). Thus, this tells us that we can arrive at the criteria directly from the first equation in the following way:
( a + b + c + d + e + f ) − ( a + b + c ) − ( c + d + e ) = ( a + b + c + d + e + f ) − ( c + d + e ) − ( e + f + a ) = ( a + b + c + d + e + f ) − ( e + f + a ) − ( a + b + c ) ⇔ f − c = b − e = d − a
Log in to reply
Relevant wiki: Composite Figures
An equiangular hexagon has six angles of 1 2 0 ∘ each. Suppose we construct an equiangular hexagon like the one in the diagram below.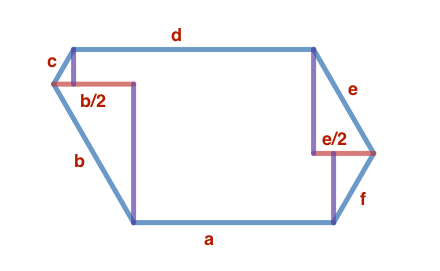
Notice that all the right triangles in the diagram have angles of
3
0
∘
,
6
0
∘
,
9
0
∘
. This means that, in each right triangle, the red horizontal sides have exactly half the length of the blue hypotenuses. Therefore, we can conclude that
d = a + 2 b + f − 2 c + e .
Rearranging, we get a − d = 2 ( c − f ) + ( e − b ) .
By starting from different sides and applying the same process, we can derive the additional equations e − b = 2 ( a − d ) + ( c − f ) , and c − f = 2 ( a − d ) + ( e − b ) .
Using substitution in this system of equations, we find that a − d = c − f = e − b . This means that the difference between the lengths of opposite sides must be equal.
Now, if our given side lengths are 1 , 2 , 3 , 4 , 5 , 6 , that means we need to find three subtraction facts with equal differences that use each one of the first six positive integers exactly once. This is only possible when the difference is 1 or 3, as follows:
6 − 5 , 4 − 3 , 2 − 1 and 6 − 3 , 5 − 2 , 4 − 1 .
Feeding the appropriate values into the equation a − d = c − f = e − b , we obtain the two unique solutions below.