A probability problem by Rajat Bhagat

Place the chessboard in the coordinate plane, so that the lower-left corner is at $(0,0$ ), and the upper-right corner is at $(8,8$ ). It is clear that ants A and B must meet at a point of the form $(k,8 - k)$ , where $0 \le k \le 8$ .

Suppose you follow ant A's path from $(0,0)$ to $(k,8 - k)$ , and then you follow ant B's path in reverse , from $(k,8 - k)$ to $(8,8)$ . Then you get a path from $(0,0)$ to $(8,8)$ .

Conversely, if you take any path from $(0,0)$ to $(8,8)$ , it must cross the line $x + y = 8$ at a unique point. Let $(k,8 - k)$ be this point. Then you can let ant A take the portion of the path from $(0,0)$ to $(k,8 - k)$ , and you can let ant B take the portion of the path from $(8,8)$ to $(k,8 - k)$ .

Thus, the number of ways that ants A and B can meet is equal to the number of paths from $(0,0)$ to $(8,8)$ , which is $\binom{16}{8} = 12870$ .

I'm assuming that the insects move along the edges.

Wlog, let the first insect ( A ) be in the bottom left corner, and the second insect ( B ) be in the top right corner. A can move only right or up, whereas B can move left or down.

When A and B meet, let A have moved $m$ units to the right and $n$ units up. Clearly, B must have moved $8-m$ units to the left and $8-n$ units down.

Now, as they move with the same speed; when they meet, they must have moved equal distances. $\therefore \ m+n=8-m+8-n \implies 2m+2n=16 \implies n=8-m$ .

Now, all we need to do is arrange these moves of A and B .

We can arrange the moves of A in $\dfrac{8!}{m!(8-m)!}=\binom{8}{m}$ ways. Similarly, we can arrange themoves of B in $\dfrac{8!}{(8-m)!m!}=\binom{8}{m}$ ways. These two will get multiplied.

Finally, what we need to do is sum these number of ways over $m$ (from $0$ to $8$ ). Therefore, the required number of ways is $\sum_{m=0}^{8} \binom{8}{m}^2=\binom{16}{8}=\boxed{12870}$

Note : The sum can be evaluated by looking for the coefficient of $x^8$ in $(1+x)^8(1+x)^8$ in two different ways. Try to do this yourself. The value is of course $\binom{16}{8}$ .

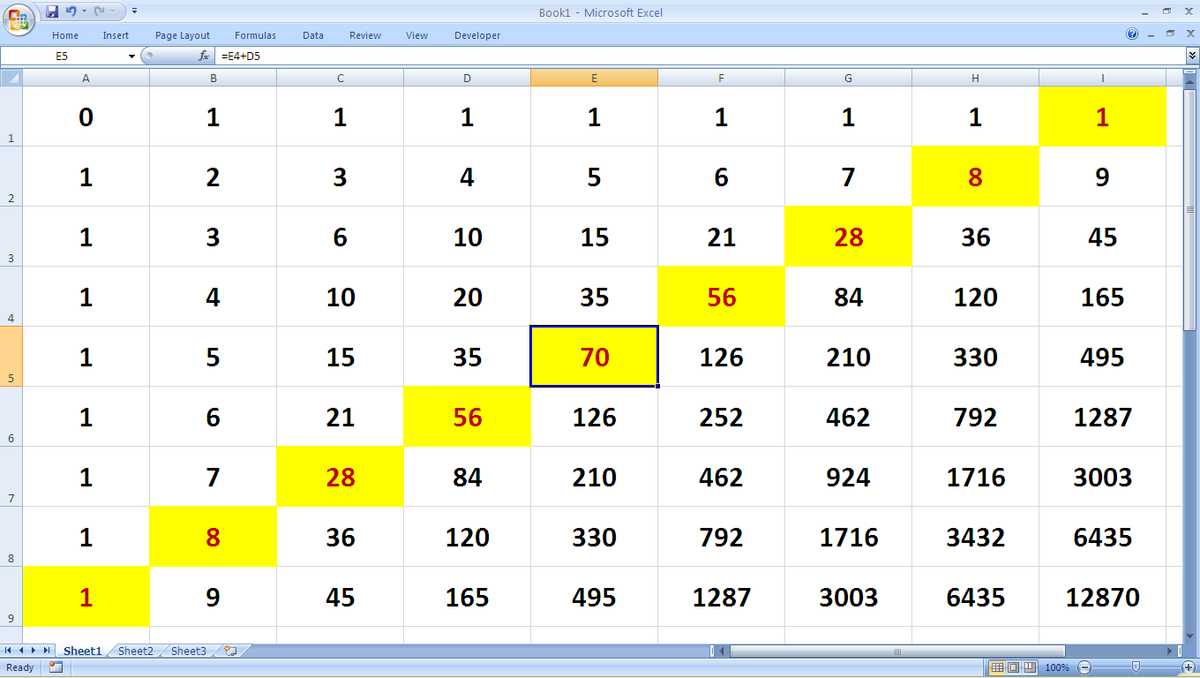
Here as the insects move along the edges, they will meet after nine moves at nine different possible places and so the problem is similar to meeting of the insects if they move on the boxes on a 9x9 chessboard. Here we know that the number of ways to reach a specific box say E5 (in Excel notation not in chess notation) from A1 is equal to the number of ways to reach the two adjacent boxes (here E4+D5) , i.e. in the image the number in each box represents the number of ways to get to that box which is actually the sum of the box above and to it's left (when we consider that insect starts from A1). I used MS-Excel to copy the formulas in all the boxes (as in excel it automatically re-adjusts to the sum of the box above and beside it ; all you have to do is to write all those 1's and write B1+A2 in B2 and then copy it)

Now the answer is simply the sum of the squares of all those coloured diagonal elements