Do you know how to solve a system of one quadratic and one linear equation?
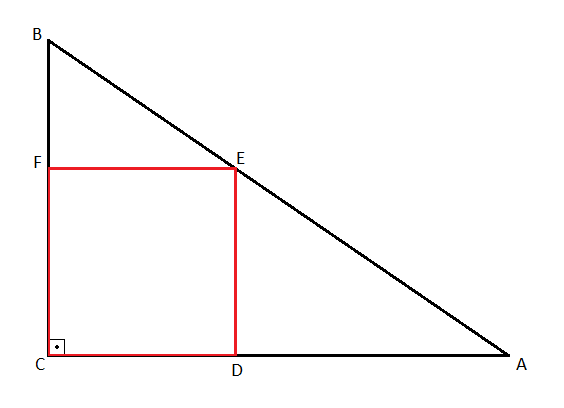
The hypotenuse of the right-angled triangle has length . The square , whose side length is , is inscribed in the triangle as shown above (pictured red).
If is the longer leg of the triangle, and is the shorter leg, find the value of .
Hint : .
The answer is 7.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
I literally just spent 1 hour writing the solution and clicked "Have the solution checked by a pro" and it took me to the Brilliant^2 site and the solution is gone. I'm too lazy to write it all again, so I'll just write the main things:
From the given hint, you notice that the legs of the two triangles are proportional.
Solving the proportion you'll conclude that 12(a+b)=ab.
From the Pythagorean theorem, we know that a^2+b^2=1225. We also know that a 2 + b 2 = ( a + b ) 2 − 2 a b so we can re-write it as (a+b)^2-2ab=1225
That gives us a system/set of two equations. We add replacements for easier solving: ab=x and a+b=y
Now the set of equations looks like this: 1 2 y = x y 2 − 2 x − 1 2 2 5 = 0
Plugging in the x from the first one into the second one, we get y 2 − 2 4 y − 1 2 2 5 = 0 Solving this quadratic equation, we get that the only positive solution for y is 49. That makes x=588. That gives us a new set of equations. a × b = 5 8 8 a + b = 4 9 Solving this, we get b=28 and a=21 (because b>a). Finally, we have: b − a = 2 8 − 2 1 b − a = 7 . 0 0