Do you know my function?
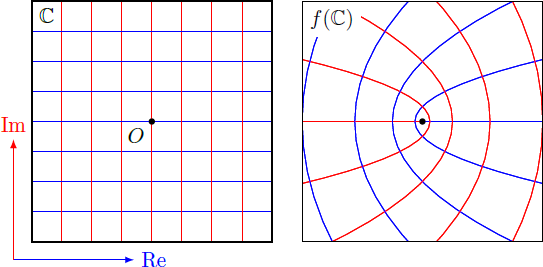
The diagram shows a complex-valued function , in the complex plane. The image of the function is illustrated as mapping of the coordinate lines (red lines) and (blue lines). The point in the middle indicates the origin of the complex plane.
Which function is it?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
f ( z ) = 2 1 z 2 = 2 1 ( x + i y ) 2 = 2 1 ( x 2 − y 2 ) + i x y Coordinate lines x = const and y = const are parabolas or square roots. For the example y = 1 gives the image of the coordinate line ( u , v ) = ( 2 1 ( x 2 − 1 ) , x ) , such that v = ± 2 u + 1 . f ( z ) = ( 2 1 + 2 i ) z = ( 2 1 + 2 i ) ( x + i y ) = ( 2 1 x − 2 y ) + i ( 2 x + 2 1 y ) Coordinate lines remain straight lines. The coordinate net is only rotated and stretched by a constant factor. f ( z ) = z 1 = x + i y 1 = x + i y 1 ⋅ x − i y x − i y = x 2 + y 2 x − x 2 + y 2 i y The complex plane is virtually inverted by this mapping. Points at infinity are mapped to the origin so that all coordinate lines intersect here. In addition, all coordinate lines are mapped to circles (can you proof this?). f ( z ) = cos ( z ) = 2 1 ( e i ( x + i y ) + e − i ( x + i y ) ) = 2 1 ( e − y + i x + e y − i x ) = 2 1 ( e − y ( cos ( x ) + i sin ( x ) ) + e y ( cos ( x ) − i sin ( x ) ) ) = cos ( x ) cosh ( y ) − i sin ( x ) sinh ( y ) The coordinate lines y = const are ellipses with semi-axes a = cosh ( y ) and b = sinh ( y ) .