Do you know point symmetry about point of inflection?
 Given that
A
3
−
3
A
2
+
5
A
−
1
=
B
3
−
3
B
2
+
5
B
−
5
=
0
.
Given that
A
3
−
3
A
2
+
5
A
−
1
=
B
3
−
3
B
2
+
5
B
−
5
=
0
.
Find the real value of A + B .
The answer is 2.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Moderator note:
There's a simpler approach to this. Hint: show that the two cubic equations are related by a suitable substitution.
Could you explain this step by step?
See my solution to an equivalent problem: Cubic Twins
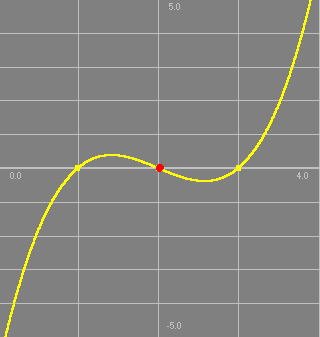
Clearly, the curve has a point symmetry about the inflection point (1,2) as
f(1+x) +f(1-x) = 4.
Hence, the sum of roots A +B =2.
Moderator note:
Hm, I fail to understand what you are trying to say. What is f ( x ) ? Unfortunately, not all of us are mind-readers, and we can only read what you have written down.
Hm, I fail to understand what you are trying to say. What is f ( x ) ? Unfortunately, not all of us are mind-readers, and we can only read what you have written down.
Log in to reply
I have taken f(x) = x^3 -3x^2 +5x - 1
Log in to reply
With that as f ( x ) , I agree that we do have f ( 1 + x ) + f ( 1 − x ) = 4 by expanding.
How does that tell us that A + B = 2 ?
You can edit your solution directly by clicking on the edit button.
Define f ( x ) = x 3 − 3 x 2 + 5 x = ( x − 1 ) 3 + 2 ( x − 1 ) + 3 .
f ( A ) − 3 = ( A − 1 ) 3 + 2 ( A − 1 )
f ( B ) − 3 = ( B − 1 ) 3 + 2 ( B − 1 )
Note that f ( A ) + f ( B ) − 6 = A 3 − 3 A 2 + 5 A + B 3 − 3 B 2 + 5 B − 6 = 0 ,
and f ( A ) + f ( B ) − 6 = ( A − 1 ) 3 + ( B − 1 ) 3 + 2 ( A + B − 2 ) .
So ( A + B − 2 ) [ ( A − 1 ) 2 − ( A − 1 ) ( B − 1 ) + ( B − 1 ) 2 + 2 ] = 0 .
Note that ( A − 1 ) 2 − ( A − 1 ) ( B − 1 ) + ( B − 1 ) 2 + 2 ≥ 2 .
Hence, A + B = 2 .