Do you know the reverse process?
f ( x ) = a x 3 + b x 2 + c x + d , where a , b , c , d ∈ N . Given that,
f
(
1
)
=
1
0
f
(
2
)
=
2
7
f
(
3
)
=
6
0
f
(
4
)
=
1
1
5
Then find ( a × b × c × d ) + ( a + b + c + d ) .
The answer is 34.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Moderator note:
Good systematic way of solving the system of linear equations.
You could have reduced some steps by directly saying that 'a' must be equal to 1 from the 4th equation , and from 'a 'belongs to natural no.s
Totally same way
In matrix, the equation system is as follows:
⎝ ⎜ ⎜ ⎛ 1 3 2 3 3 3 4 3 1 2 2 2 3 2 4 2 1 2 3 4 1 1 1 1 ⎠ ⎟ ⎟ ⎞ ⎝ ⎜ ⎜ ⎛ a b c d ⎠ ⎟ ⎟ ⎞ ⇒ ⎝ ⎜ ⎜ ⎛ 1 8 2 7 6 4 1 4 9 1 6 1 2 3 4 1 1 1 1 ⎠ ⎟ ⎟ ⎞ ⎝ ⎜ ⎜ ⎛ a b c d ⎠ ⎟ ⎟ ⎞ ⇒ ⎝ ⎜ ⎜ ⎛ a b c d ⎠ ⎟ ⎟ ⎞ ⇒ a b c d + a + b + c + d = ⎝ ⎜ ⎜ ⎛ 1 0 2 7 6 0 1 1 5 ⎠ ⎟ ⎟ ⎞ = ⎝ ⎜ ⎜ ⎛ 1 0 2 7 6 0 1 1 5 ⎠ ⎟ ⎟ ⎞ = ⎝ ⎜ ⎜ ⎛ 1 8 2 7 6 4 1 4 9 1 6 1 2 3 4 1 1 1 1 ⎠ ⎟ ⎟ ⎞ − 1 ⎝ ⎜ ⎜ ⎛ 1 0 2 7 6 0 1 1 5 ⎠ ⎟ ⎟ ⎞ = 6 1 ⎝ ⎜ ⎜ ⎛ − 1 9 − 2 6 2 4 3 − 2 4 5 7 − 3 6 − 3 2 1 − 4 2 2 4 1 − 6 1 1 − 6 ⎠ ⎟ ⎟ ⎞ ⎝ ⎜ ⎜ ⎛ 1 0 2 7 6 0 1 1 5 ⎠ ⎟ ⎟ ⎞ = ⎝ ⎜ ⎜ ⎛ 1 2 4 3 ⎠ ⎟ ⎟ ⎞ = 2 4 + 1 0 = 3 4
I used the following Excel spreadsheet to do the calculations.
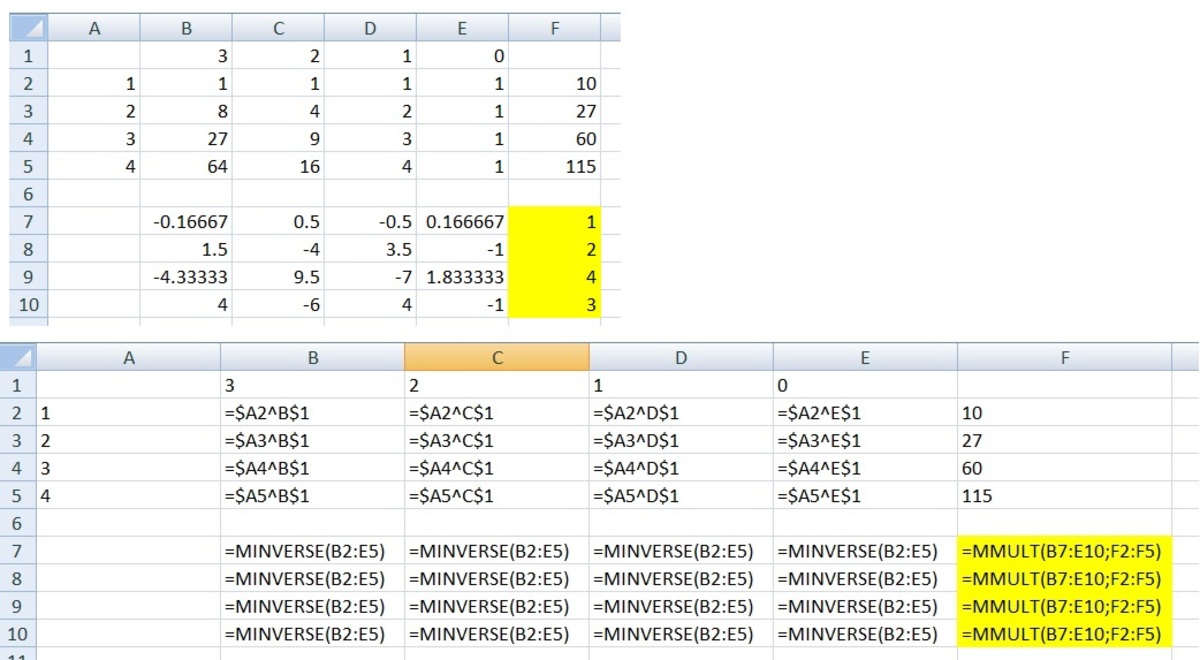
There seems to be a typo.
The correct solution has c=4 and d=3
That does not affect the answer, though.
Log in to reply
Thanks, you are right. I have edited the solution.
We will use Lagrange interpolation discussed here
Let f ( x ) = p ( x − 1 ) ( x − 2 ) ( x − 3 ) + q ( x − 1 ) ( x − 2 ) ( x − 4 ) + r ( x − 1 ) ( x − 3 ) ( x − 4 ) + s ( x − 2 ) ( x − 3 ) ( x − 4 )
Put f ( 1 ) = 1 0 We get s = 3 − 5
Similarly putting f ( 2 ) = 2 7 , f ( 3 ) = 6 0 , f ( 4 ) = 1 1 5 yields respectively the values
r = 2 2 7 , q = − 3 0 , p = 6 1 1 5
Put in f ( x ) to get
f ( x ) = 6 1 1 5 ( x 3 − 6 x 2 + 1 1 x − 6 ) − 3 0 ( x 3 − 7 x 2 + 1 4 x − 8 ) + 2 2 7 ( x 3 − 8 x 2 + 1 9 x − 1 2 ) − 3 5 ( x 3 − 9 x 2 + 2 6 x − 2 4 )
f ( x ) = x 3 + 2 x 2 + 4 x + 3
Clearly a = 1 , b = 2 , c = 4 , d = 3
a . b . c . d = 2 4 and a + b + c + d = 1 0
A n s w e r = 2 4 + 1 0 = 3 4
f ( 1 ) ⇒ f ( 2 ) ⇒ f ( 3 ) ⇒ f ( 4 ) ⇒ a ( 1 ) 3 + b ( 1 ) 2 + c ( 1 ) + d ⇒ a ( 2 ) 3 + b ( 2 ) 2 + c ( 2 ) + d ⇒ a ( 3 ) 3 + b ( 3 ) 2 + c ( 3 ) + d ⇒ a ( 4 ) 3 + b ( 4 ) 2 + c ( 4 ) + d ⇒ a + b + c + d 8 a + 4 b + 2 c + d 2 7 a + 9 b + 3 c + d 6 4 a + 1 6 b + 4 c + d = 1 0 = 2 7 = 6 0 = 1 1 5 ⇒ ( 1 ) ⇒ ( 2 ) ⇒ ( 3 ) ⇒ ( 4 )
( 2 ) − ( 1 ) ; ( 3 ) − ( 2 ) ; ( 4 ) − ( 3 ) ; 7 a + 3 b + c 1 9 a + 5 b + c 3 7 a + 7 b + c = 1 7 = 3 3 = 5 5 ⇒ ( 5 ) ⇒ ( 6 ) ⇒ ( 7 )
( 6 ) − ( 5 ) ; ( 7 ) − ( 6 ) ; 1 2 a + 2 b 1 8 a + 2 b = 1 6 = 2 2 ⇒ ( 8 ) ⇒ ( 9 )
( 9 ) − ( 8 ) ; 6 a = 6 ⇒ a = 1
Instead a with 1 in equation ( 8 ) ;
1 2 ( 1 ) + 2 b 2 b = 1 6 = 4 ⇒ b = 2
Instead a with 1 and b with 2 in equation ( 5 ) ;
7 ( 1 ) + 3 ( 2 ) + c 1 3 + c = 1 7 = 1 7 ⇒ c = 4
Instead a with 1 , b with 2 and c with 4 in equation ( 1 ) ;
1 + 2 + 4 + d 7 + d = 1 0 = 1 0 ⇒ d = 3
Thus, ( a ⋅ b ⋅ c ⋅ d ) + ( a + b + c + d ) = ( 1 ⋅ 2 ⋅ 4 ⋅ 3 ) + 1 0 = 2 4 + 1 0 = 3 4