Do you know your exponents?
2 3 + 2 3 + 3 4 + 3 4 + 3 4 = ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
20 solutions
Nice and simply method! ;-) I find it easy. 😊😊
2³ is being added twice so it is multiplied by 2, therefore it is 2³×2=2^4. And 3^4 is being addedthree times so it is multiplied by 3, therefore 3^4×3=3^5. So the answer is 2^4+3^5
Great shortcut :)
Log in to reply
Another way is 2^3=8 so you have 2*8 = 16 and 2^4 is 16
this is a wrond method
Log in to reply
..then what's the right method? How about some constructive criticism?
( 2 3 + 2 3 ) + ( 3 4 + 3 4 + 3 4 ) . There are 2 2 3 's so they can be rewritten as 2 ( 2 3 ) . There are 3 3 4 so they can be rewritten as 3 ( 3 4 ) . Because the 2 in front of 2 ( 2 3 ) has the same base as the 2 3 ) on the inside, the exponents can be added (the 2 has an implied 2 1 ). The same can be done for the 3 in front of the 3 ( 3 4 ) which has an implied 3 1 . This means that the 2 ( 2 3 ) simplifies to 2 4 and the 3 ( 3 4 ) becomes 3 5 . Now the addition of these two is 2 4 + 3 5 .
This it the only one that actually explains how the solution came about. Thank you for that. Now I understand it where following the math of the others I was not getting it.
the given value's sum is 259 and only option (a) satisfies it
Yes, that is one way. See Wahyu's solution above for what I was thinking about.
(2^3+2^3)+(3^4+3^4+3^4) =2.2.2.(1+1)+3.3.3.3.(1+1+1) =2.2.2.2 + 3.3.3.3.3 =2^4 + 3^5
2^3 + 2^3 +3^4 +3^4 +3^4
=2^3 x 2 + 3^4 x 3
=2^4 +3^5........................................[2=2^1 and 3=3^1]
2 3 + 2 3 + 3 4 + 3 4 + 3 4
= 2 3 ( 1 + 1 ) + 3 4 ( 1 + 1 + 1 )
= 2 3 ( 2 ) + 3 4 ( 3 )
= 2 4 + 3 5
2 3 + 2 3 + 3 4 + 3 4 + 3 4 = 2 3 ( 1 + 1 ) + 3 4 ( 1 + 1 + 1 ) = 2 3 × 2 + 3 4 × 3 = 2 3 + 1 + 3 4 + 1 = 2 4 + 3 5
2³*2 = 2³ + 2³ = 2²+² ||| 3²+² *3 = 3²+² + 3²+² + 3²+²
2 3 + 2 3 + 3 4 + 3 4 + 3 4
= ( 2 ⋅ 2 3 ) + ( 3 ⋅ 3 4 )
= 2 4 + 3 5
2 3 + 2 3 + 3 4 + 3 4
= 2 × 2 3 + 3 × 3 4
= 2 4 + 3 5
First, we can take 2^3, & 3^4 as a common value, i.e,
2^3 (1+1)+3^4 (1+1+1)
Afterwards, we can take it as,
2^3 (2)+3^4 (3)
Now, we know that when base is same, powers add up..so the result will be:
2^4+3^5
let 2^3=a,3^4=b =a+a+b+b+b=2a+3b =2(2^2)+3(3^4) =2^3+3^5(law of exponent:a^b*a=a^b+1 )
The sum is 2 times 2^3 and 3 times 3^4 = 2.2^3 + 3.3^4 = 2^(1+3) + 3^(1+4)= 2^4 + 3^5
2^3 + 2^3 + 3^4 + 3^4 + 3^4
= 2(2^3) + 3(3^4)
2 = 2^1 and 3 = 3^1
= 2^1 * 2^3 + 3^1 * 3^4
Product rule : a^n * a^m = a^(n+m)
Therefore:
2^1 * 2^3 = 2^4
And:
3^1 * 3^4 = 3^5
=2^4 + 3^5
2^3+2^3+3^4+3^4+3^4 =2.2^3+3.3^4 =2^4+3^5
2^3+2^3=2^3(1+1)
=2^3*2=2^4
3^4+3^4+3^4=3^4(1+1+1)
=3^4(3)
=3^5
2^4+3^5
this is one of the easiest problems to me for solving this kind of problems you must know how to take common. in this problem we will take 2^3 and 3^4 common
Thanks for writing a solution!
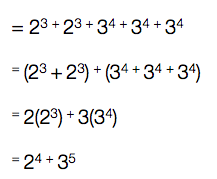
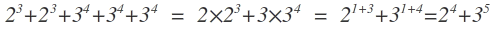
Using the Rules of Exponents :
2 3 + 2 3 + 3 4 + 3 4 + 3 4
= 2 3 ( 1 + 1 ) + 3 4 ( 1 + 1 + 1 )
= 2 3 ( 2 ) + 3 4 ( 3 )
= 2 4 + 3 5