Do You Know Your Quadrants?
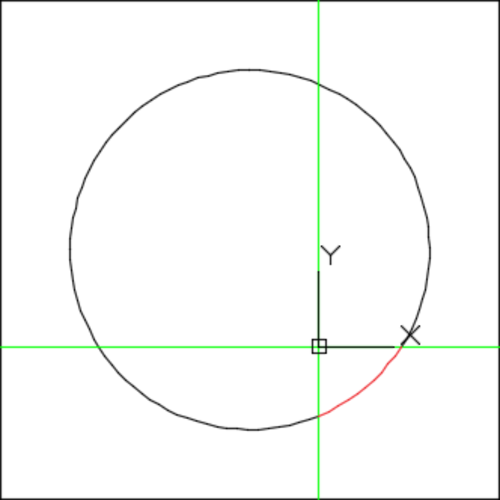
What percentage of the circumference of the circle above is in the fourth quadrant of the xy plane?
Round your answer to 3 correct decimal places.
The answer is 9.667.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First, we need to find the intersection of the circle and the x and y axes. This can be done more easily by converting the equation of the circle to its standard form.
( x 2 + y 2 + 1 0 x − 1 4 y − 9 5 = 0 ⇒ ( x 2 + 1 0 x + 5 2 ) + ( y 2 − 1 4 y + 7 2 ) = 9 5 + 5 2 + 7 2 ⇒ ( x + 5 ) 2 + ( y − 7 ) 2 = 1 6 9
Now we can find the x and y intercepts by setting y to 0 and x to 0 respectively.
( x + 5 ) 2 + ( 0 − 7 ) 2 = 1 6 9 ⇒ ( x + 5 ) 2 = 1 2 0 ⇒ x = − 5 ± 1 2 0 ( 0 + 5 ) 2 + ( y − 7 ) 2 = 1 6 9 ⇒ ( y − 7 ) 2 = 1 4 4 ⇒ y = 7 ± 1 2
The x values are positive and the y values are negative in quadrant I V , so we're left with ( 0 , − 5 ) and ( 1 2 0 − 5 , 0 ) as our intersection points. Now, to find the amount of the circle's circumference in the fourth quadrant, we simply need to find the angle between the lines formed by the intersection points and the center of the circle at ( − 5 , 7 ) . To do this, we first need to find the slopes of such lines.
For the line connecting the center of the circle to the y-intercept at ( 0 , − 5 ) , we have a slope of m 1 = − 5 1 2 . For the other line, we have a slope of m 2 = − 1 2 0 7
Finally, we now have the slopes, so we can now find the angle between the lines.
tan ( θ ) = 1 + m 2 m 1 m 2 − m 1 = 1 2 7 3 0 − 3 0 ⇒ θ ≈ 3 4 . 8 0 1 °
The entire circle has an angle of 360 degrees, so just simply divide theta by 360 to get the percentage, so the answer is ≈ 9 . 6 6 7 percent, correct up to 3 decimal places.