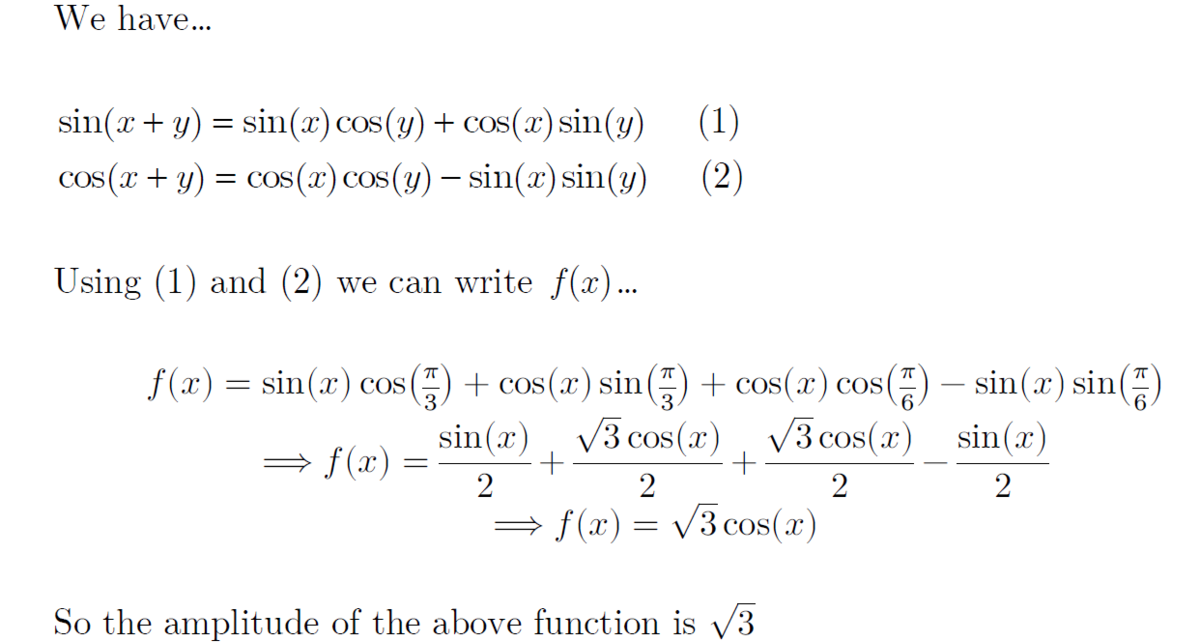Do You Know Your Trig Graphs?
What is the amplitude of the graph of f ( x ) = sin ( x + 3 π ) + cos ( x + 6 π ) ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
This becomes sin ( x + π / 3 ) + sin ( π / 2 − x − π / 6 )
= sin ( x + π / 3 ) + sin ( π / 3 − x )
= 2 sin ( π / 3 ) cos x
The amplitude of the above function is 2 sin ( π / 3 ) = 3
The sum of any 2 sine or cosine wave with the same wavelength acquire maximum or minimum amplitude at their intersection. For instance, 2sin; 0 phase difference; intersect at 0; altitude=2sin(0). Another example, sin+cos; 90 phase difference; intersect at 45 deg; altitude=2sin(45). The problem above has phase difference of 60 degree. Therefore the altitude is 2sin(60/2). So the answer is 2*root(3)/2 = root(3). :)
Wait how 2sin(60/2) equals root(3) it must have been equal to 1
How does that help in knowing the amplitude....???!!!
Log in to reply
It gives the right answer, indeed. But i'm not really sure that it's applicable to all problems of such kind.