Do you like ellipse?
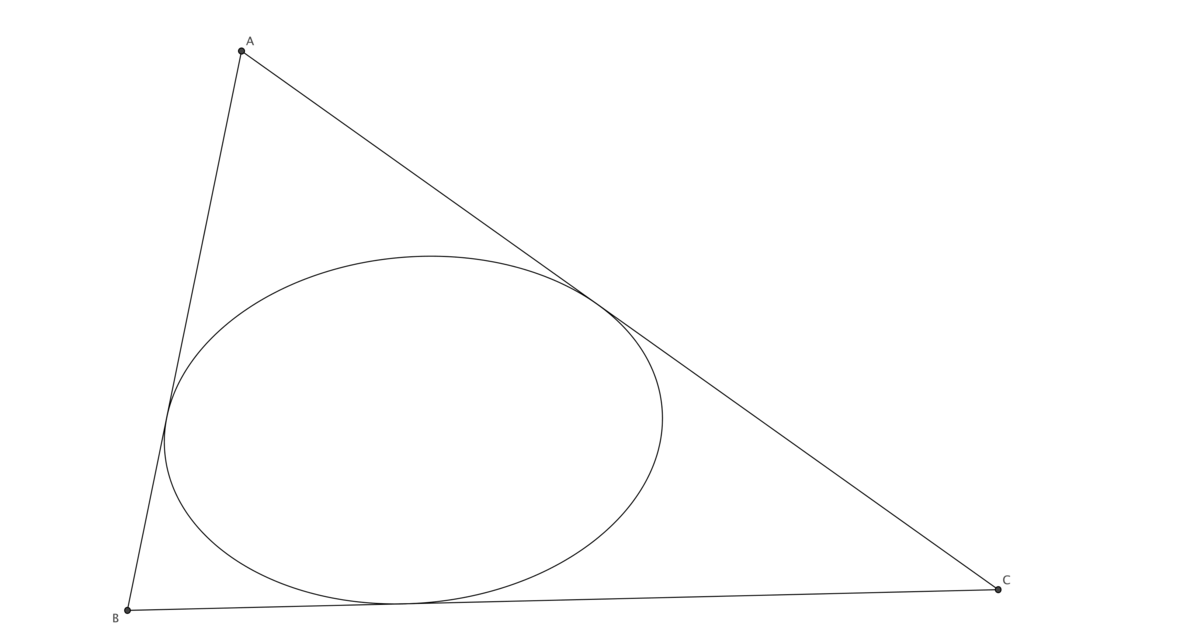
Let k be the ratio of the area of an ellipse A e to the area of the triangle A t the ellipse is inscribed in; that is: k = A t A e .
Given that the maximum value of k has a closed form, find this closed form.
Submit your answer to 2 decimal places.
The answer is 0.60.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Can you please give a more detailed solution ! Thanks.
link text
This is known as Steiner_inellipse and the above link gives us that the ratio is
3
3
π
.
This link is from my solution to almost the same problem "Medial Ellipse" by Sharky Kesa, just two days back.
The ellipse is Steiner inellipse . The ratio is 3 3 π ≈ 0 . 6 0
Project the plane such that the ellipse becomes the circle, in this projection ratio of areas are invariant!
⟹ k = ( Δ π r 2 ) = ( s 2 Δ π Δ 2 ) = ( s 2 π Δ )
w.l.o.g assume s=1 ⟹ a+b+c=2
⟹ π Δ = π ( ( 1 − a ) ( 1 − b ) ( 1 − c ) ) ≤ π ( 3 ( 1 − a ) + ( 1 − b ) + ( 1 − c ) ) 2 3 = 3 3 π u s i n g A M − G M ⟹ M A X k = 3 3 π ≈ 0 . 6 0