Do You Like Powers?
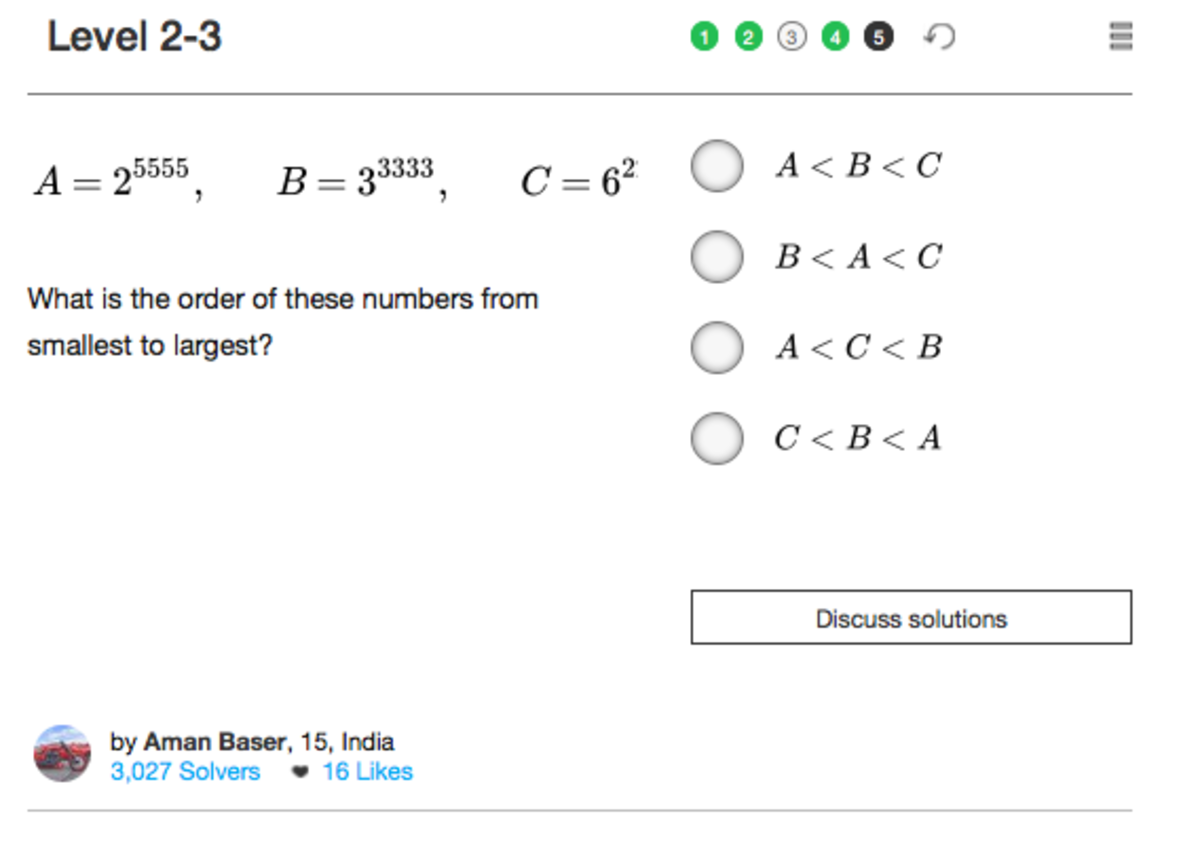
A = 2 5 5 5 5 , B = 3 3 3 3 3 , C = 6 2 2 2 2
What is the order of these numbers from smallest to largest?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
the last number was presented as 6^2
Log in to reply
just scroll the tab to the left... I had the same problem. Annoying
I have the right answer, but...You know how your mouse pad starts freaking out because it gets wet? Never do math problems while eating grease food. Your mouse pad might screw you over. Hate my life.
A = ( 2 5 ) 1 1 1 1 , B = ( 3 3 ) 1 1 1 1 , C = ( 6 2 ) 1 1 1 1 2 5 = 3 2 , 3 3 = 2 7 , 6 2 = 3 6 . ∴ B < A < C .
Did the same way
Easiest explaination.
wow! really excellent solution
Fine solution.....
In this entire solution, all the lo g functions are in base-10.
We know that lo g ( 2 ) = 0 . 3 0 1 , lo g ( 3 ) = 0 . 4 7 7 .
lo g ( A ) = 5 5 5 5 lo g ( 2 ) = 5 5 5 5 × 0 . 3 0 1 ≈ 1 6 7 2 . 2
lo g ( B ) = 3 3 3 3 lo g ( 3 ) = 3 3 3 3 × 0 . 4 7 7 ≈ 1 5 9 0 . 2
lo g ( C ) = 2 2 2 2 lo g ( 6 ) = 2 2 2 2 ( lo g ( 2 ) + lo g ( 3 ) ) = 2 2 2 2 ( 0 . 3 0 1 + 0 . 4 7 7 ) ≈ 1 7 2 9 . 1
Since we can see that lo g ( C ) > lo g ( A ) > lo g ( B ) and since A , B , C > 0 , we conclude that C > A > B .
did the same way, logarithms make the things so easy
I've used logarithms too!
A has 1673 digits.
B has 1591 digits.
C has 1730 digits.
Clearly C>A>B
what math did you use to get the digits ? I wonder how you do it,
Log in to reply
using logarithm.. for example 2^x has X lo2+1 no of digits. here we take log to base 10. for example 2^10 has 10 log2 to base 10+1 digits= 10*.3010+1= 4. we take only the integer part of the product. hope its clear!
It would be better at this level to explain how you get the digits. However I like your approach, though it may not work always.
Log in to reply
Using logarithm, i found the number of digits as, log2^5555 + 1 and two others
How can I find the No. of digits??? Please explain me...
Log in to reply
just take log base 10 and add 1
hw did u find out the digits?
hw did u find out the digits?
How to find no of digits
Log in to reply
using logarithm.. for example 2^x has X lo2+1 no of digits. here we take log to base 10. for example 2^10 has 10 log2 to base 10+1 digits= 10*.3010+1= 4. we take only the integer part of the product. hope its clear!
dev, how did you calculate the number of digits?
Log in to reply
using logarithm.. for example 2^x has X lo2+1 no of digits. here we take log to base 10. for example 2^10 has 10 log2 to base 10+1 digits= 10*.3010+1= 4. we take only the integer part of the product. hope its clear!
how to calculate the number of digits?
2^5 = 32; 3^3= 27; 6^2 = 36; 27 < 32< 36 So, B<A<C.
The screen capture is only 6^2
That's why I put C<B<A and it's not correct ;-; I was like "what"?
First we can consider only one digit of power. Then calculate, 2^5=32; 3^3=27; 6^2=36.So B<A<C.
it's some what logical question: 2^5= 32 ; 3^3= 27 ; 6^2=36
We can simply look for assessment of A=3^2 ,B=3^3. c=6^2 that give us clue that C is lowest,A is more tha C and B is biggest ,therefore B <A<C
2^(5)1111 3^(3)1111 & 6^(2)*1111 Therefore, 32^1111 27^1111 36^1111 ,i jus focused on thr values of base,i don't mind the exponents coz they are just similar :D
exponents are just s a m e not only similar.
Bring all the number to the power of 1111 and then compare .

2 5 5 5 5 = 3 2 1 1 1 1
3 3 3 3 3 = 2 7 1 1 1 1
6 2 2 2 2 = 3 6 1 1 1 1
Since 2 7 < 3 2 < 3 6 , the required order of the three numbers is
3 3 3 3 3 , 2 5 5 5 5 , 6 2 2 2 2