Do you need a hint?
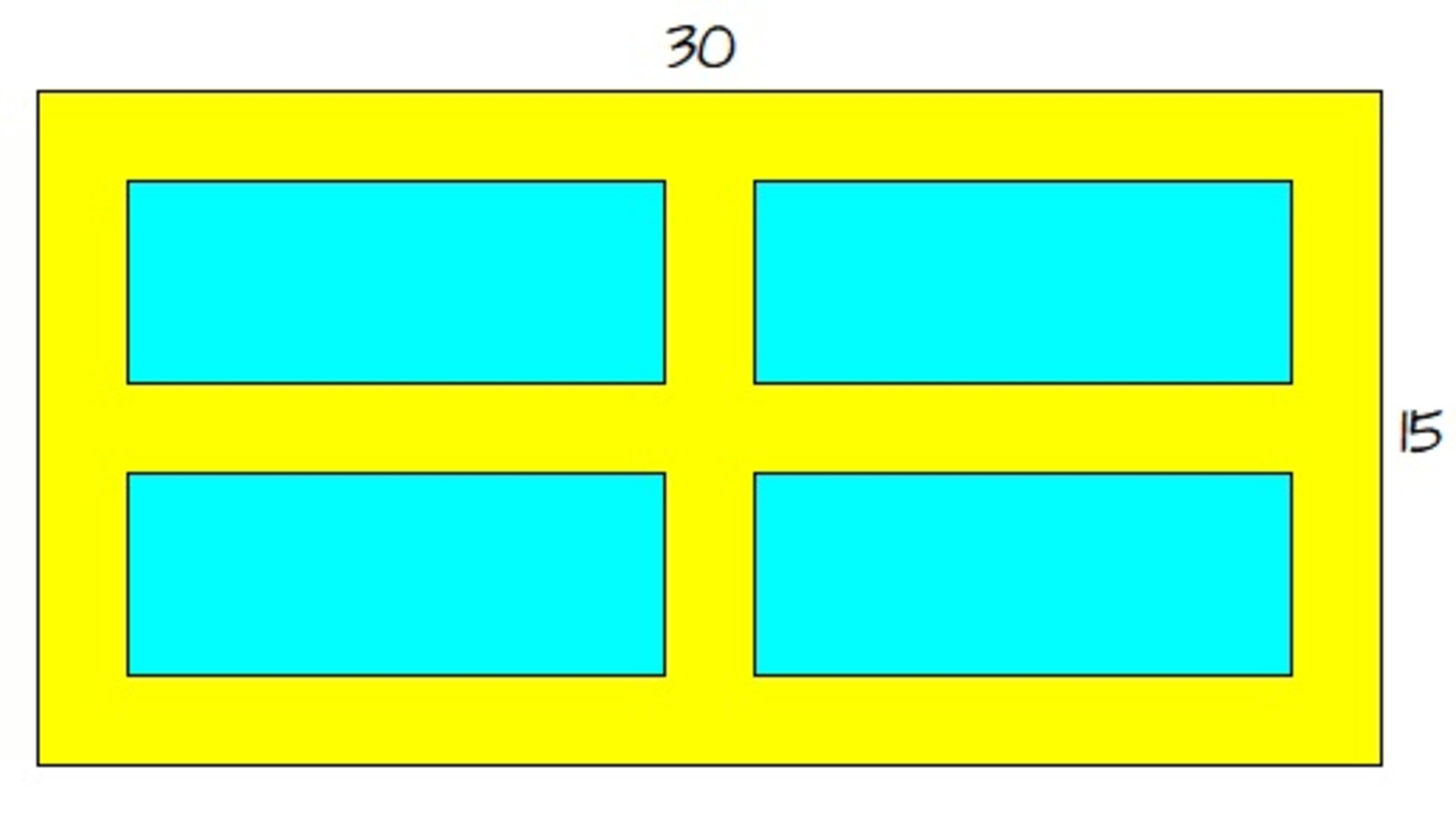 Four congruent blue rectangles are symmetrically placed inside a
rectangle such that the yellow region has a uniform width as shown in the figure. If the area of the yellow region is
, what is the longer dimension of each of the blue rectangle?
Four congruent blue rectangles are symmetrically placed inside a
rectangle such that the yellow region has a uniform width as shown in the figure. If the area of the yellow region is
, what is the longer dimension of each of the blue rectangle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 a + 2 y = 3 0 or 3 a = 3 0 − 2 y
and
3 a + 2 x = 1 5 or 3 a = 1 5 − 2 x
Since 3 a = 3 a , we have
3 0 − 2 y = 1 5 − 2 x
x = 2 2 y − 1 5 ⟹ 1
The area of the four blue rectangles is 3 0 ( 1 5 ) − 2 3 4 = 2 1 6 . So the area of one blue rectangle is
x y = 4 2 1 6 = 5 4 ⟹ 2
Now substitute 1 in 2 , we have ( 2 2 y − 1 5 ) ( y ) = 5 4
2 y 2 − 1 5 y = 1 0 8
By using the quadratic formula, we get
y = 1 2