Do you play dice games?

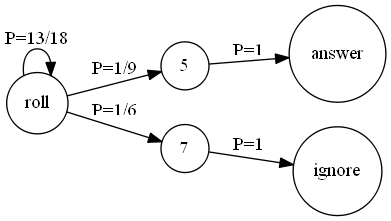
The probability of an outcome of $5$ is $\frac{1}{9}$ , and the probability of an outcome of $7$ is $\frac{1}{6}$ . Thus the probability of an outcome other than $5$ or $7$ is

$1 - (\frac{1}{9} + \frac{1}{6}) = \frac{13}{18}$ .

We now need to calculate the sum of the probabilities of getting an outcome other than $5$ or $7$ for $k$ throws and then throwing a $5$ on the $(k + 1)$ st throw, where $k$ goes from $0$ to $\infty$ . This sum will be

$\frac{1}{9} + (\frac{13}{18})(\frac{1}{9}) + (\frac{13}{18})^{2}(\frac{1}{9}) + ..... =$

$(\frac{1}{9}) * \sum_{k=0}^\infty (\frac{13}{18})^{k} =$

$(\frac{1}{9}) * \dfrac{1}{1 - \frac{13}{18}} = (\frac{1}{9})(\frac{18}{5}) = \frac{2}{5} = \boxed{0.4}$ .

Alternately, we could use conditional probabilities. Someone else would roll the dice repeatedly until they get an outcome of either $5$ or $7$ . They would inform us of this event, without telling us which outcome occurred. We would then ask ourselves, "Given that an outcome of $5$ or $7$ has occurred, what is the probability that it is a $5$ ?"

We would then use Baye's Theorem to find that

P(outcome of $5$ | a $5$ or $7$ has been rolled) =

$\dfrac{P(5)}{P(5) + P(7)} = \dfrac{\frac{1}{9}}{\frac{1}{9} + \frac{1}{6}} = \dfrac{\frac{1}{9}}{\frac{5}{18}} = \dfrac{2}{5} = 0.4$ , as found before.

Not that it's practical, you can also model this as a Markov chain.

The transition probabilities for this chain are given by the following matrix:

We can take the infinite power of this matrix and then extract the third element in the first row, corresponding to the 'absorption' following the appearance of a five. It's 0.4.

I would never trust myself to do it this way! Or at least not without checking the result with some form of Monte Carlo code like this: