Do you remember Circles?
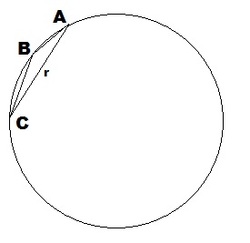 Find the magnitude of angle ABC in degrees if the radius of the circle is "r".
Find the magnitude of angle ABC in degrees if the radius of the circle is "r".
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
mhm... I figured out by drawing it's 150 but I still don't get the proof... can you elaborate a little ?
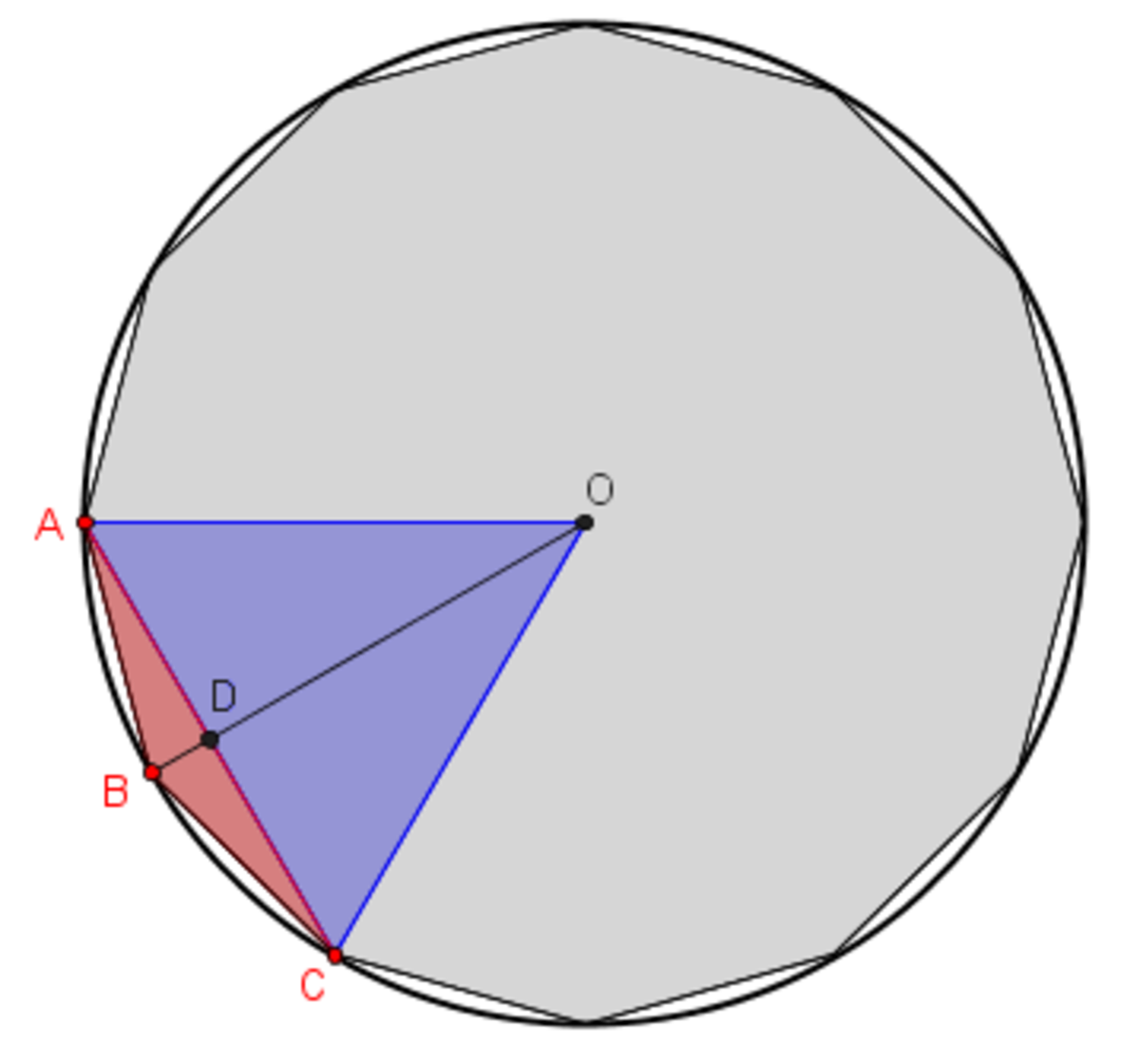
△ O A C is equilateral and O D is a perpendicular bisector to chord A C . O D is extended to point B so points O , D , B are collinear. △ A B D ≅ △ C B D by SAS congruence. This proves A B ≅ C B citing corresponding parts of congruent triangles. △ A B C is therefore isosceles. We can now conclude that we just inscribed 6 1 of a regular polygon inside the circle (i.e., 3 6 0 ∘ 6 0 ∘ ). ∠ A B C is therefore the interior angle of a regular dodecagon since we can repeat this construction 6 times in total.
∴ 1 5 0 ∘
It is not mentioned that O,D,B are collinear
If O be the centre of the circle then triangle AOC is equilateral and hence / AOC=60° which makes / ABC=150. This should be a Level 1 problem with a lesser weightage.