Do you remember this theorem?
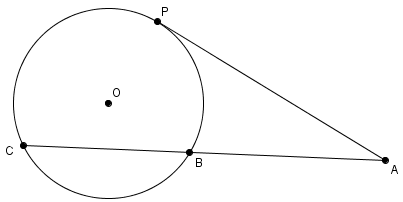
In the figure, A P is tangent to the circle centered at O , A B = B C , and A P = 3 2 . Find the length of A C .
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Good solution!
Thank you. A former brilliant member? That is me, I deleted my old account and created a new one.
Let be A B = x and A C = 2 x
A P 2 = A B ⋅ A C
( 3 2 ) 2 = 2 x ⋅ x ⇒ x 2 = 9 ⇒ x = 3
∴ A C = 6
By the power of a point,
( P A ) 2 = ( A B ) ( A C )
( 3 2 ) 2 = A B ( 2 A B )
A B = 3
Therefore, A C = 6 .
This can be found on Euclid's Elements: Book 3: Proposition 36.
By the power of a point, we have
( A P ) 2 = ( A C ) ( A B )
( 3 2 ) 2 = ( A B + A B ) ( A B )
1 8 = 2 ( A B ) 2
9 = ( A B ) 2
3 = A B
It follows that A C = 3 + 3 = 6
We know by Power of a Point that (in this case): A C ⋅ A B = A P 2 . If A P = 3 2 , then A P 2 = 1 8 . We now know that A C ⋅ A B = 1 8 . Let's set length A B = y and A C = 2 y since A B = B C Now we can form an equation and solve for y :
2 y 2 = 1 8
y 2 = 9
y = 3 .
We know that y = 3 works, so multiplying A C ⋅ A B gives us 6 ⋅ 3 = 1 8 , so length A C = 6
Relevant wiki: Power of a Point
( A P ) 2 = ( A B ) ( A C )
Substituting, we get
( 3 2 ) 2 = ( A B ) ( A C )
However, A B = B C , therefore, A C = 2 A B , so
9 ( 2 ) = ( A B ) ( 2 A B )
1 8 = 2 ( A B ) 2
9 = ( A B ) 2
3 = A B
Finally,
A C = 2 A B = 2 ( 3 ) = 6