Do you want some chocolates?
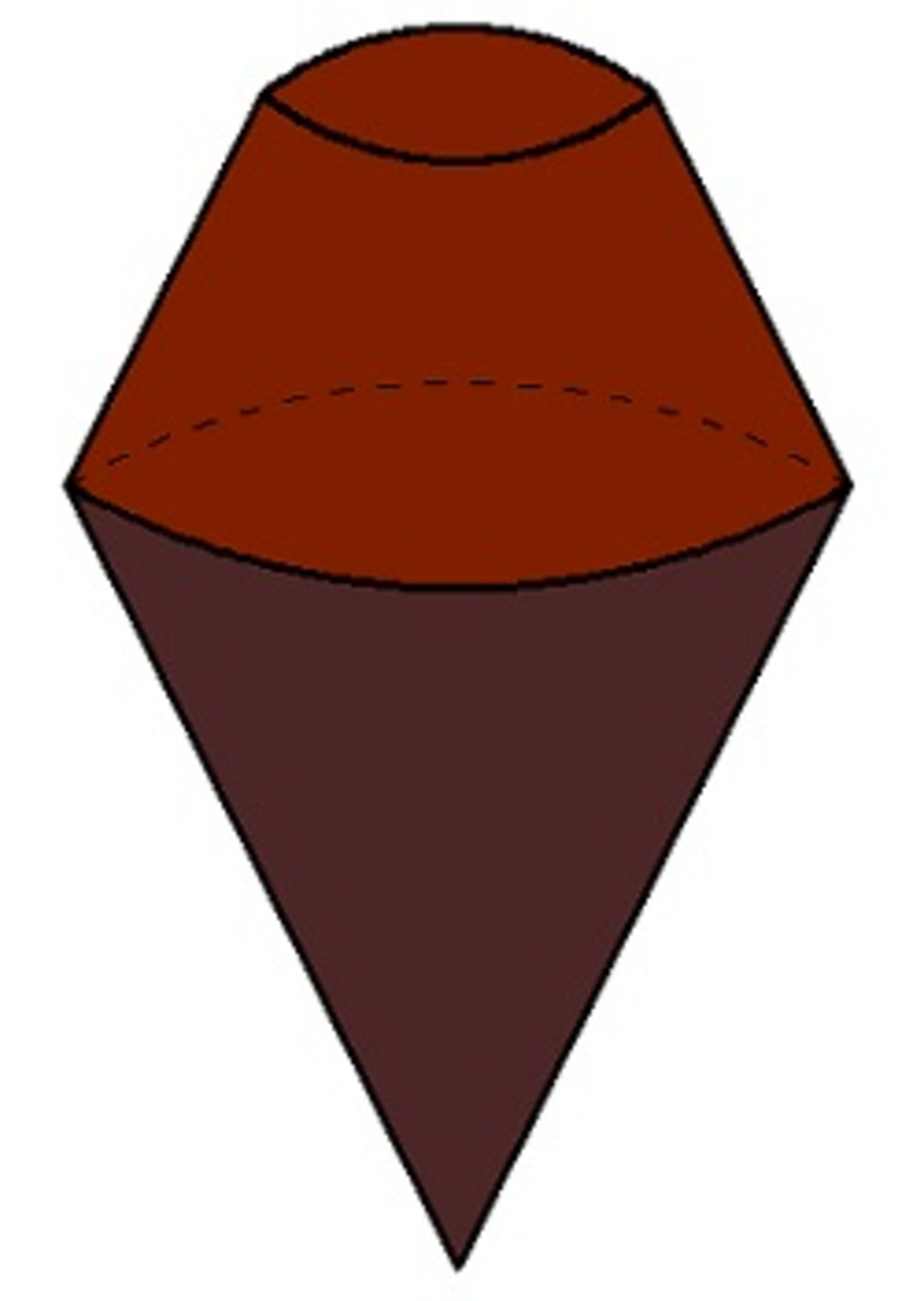The figure shown above is a special chocolate. The lower part is dark chocolate in the form of a cone with a volume of
and a height of
. The upper part is milk chocolate in the form of a frustum of a cone with a volume of
and a height of
. What is the surface area of the special chocolate? Give your answer correct to two decimal places. (Take
)
The answer is 327.10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
L o w e r p a r t : − 3 π ∗ 2 5 0 = 3 π ∗ R 2 ∗ 1 0 . ⟹ R = 5 . S l a n t a r e a A = π ∗ R ∗ 5 2 + 1 0 2 = 7 2 2 ∗ 2 5 ∗ 5 U p p e r p a r t : − 1 2 π ∗ 8 7 5 = 3 π ∗ 5 ∗ ( 2 5 + r 2 + 5 ∗ r ) S o l v i n g t h e q u a d r a t i c i n r , r > 0 , s o r = 2 5 . S i n c e t h e r a d i u s d e c r e a s e s t o h a l f f o r a h e i g h t 5 , f o r a h e i g h t o f 1 0 , i t w i l l b e a f u l l c o n e l i k e t h e L o w e r p a r t . S o t h e u p p e r p a r t = 4 3 ∗ L o w e r p a r t . . S l a n t a r e a w i l l a l s o b e = 4 3 A T o p f l a t s m a l l c i r c l e a r e a = π ∗ ( 2 2 5 ) 2 . ∴ R e q u i r e d a r e a = T o t a l s l a n t a r e a + t o p f l a t s m a l l c i r c l e a r e a . R e q u i r e d a r e a = A + 4 3 ∗ A + 4 2 5 ∗ 5 = 7 2 2 ∗ 2 5 ∗ 5 ∗ ( 1 + 4 3 ) + π ∗ ( 2 5 ) 2 . = 3 2 7 . 1 0 . .