What Law Of Reflection?

Classical Mechanics Level 3

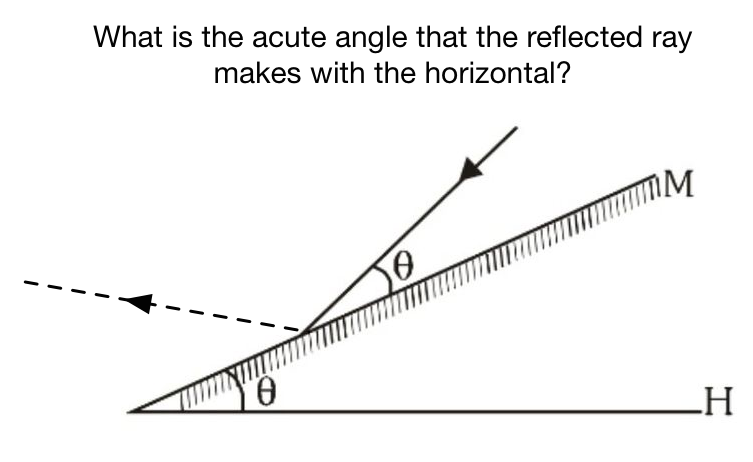
A mirror is inclined at an angle of θ \theta with the horizontal. If a ray of light is incident at an angle θ \theta as shown, then find the acute angle made by reflected ray with the horizontal.

0 0 θ \theta 2 θ 2\theta π 2 \dfrac{\pi}{2} θ 2 \dfrac{\theta}{2} None of these choices

Akhil Bansal by Akhil Bansal , 22, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Swapnil Das
Oct 25, 2016

Let the required angle be α \alpha . From the given diagram, it is clear that α + θ + ( 90 − θ ) = 90. \alpha + \theta + (90-\theta) = 90. , where the angles are in degrees.

Thus, α = 0 \alpha=0

1 Helpful 0 Interesting 0 Brilliant 0 Confused

It should be α = 0 \alpha = 0 .

Anik Mandal - 4 years, 7 months ago

Log in to reply

Thanks, that was a late night effect :P

Swapnil Das - 4 years, 7 months ago

Log in to reply

Experiencing late nights..:P

Anik Mandal - 4 years, 7 months ago

The question can be easily solved if we draw a line perpendicular to the inclined plane.

According to the first law of reflection, the angle of incidence and the angle of reflection are equal. So the reflected ray will also make an angle θ \theta but with the plane .

The point to be noted is that that is what exactly the hoizontal line does, i.e. make an angle of θ \theta with the plane. And so, the reflected ray is parallel to the horizontal direction.

Hence the answer is 0 ∘ {0}^{\circ} .

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...