Dodecagon Folding

Regular dodecagon $ABCDEFGHIJKL$ has unit sides, and diagonals $BD$ , $FH$ , $JL$ , $AE$ , $EI$ , and $IA$ are drawn as shown.

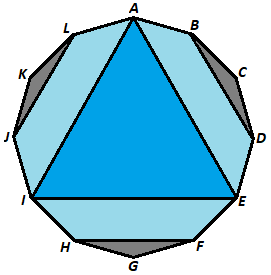
Triangles $\triangle BCD$ , $\triangle FGH$ , and $\triangle JKL$ are cut out and discarded. Trapezoids $ABDE$ , $EFHI$ , and $IJLA$ are folded up along diagonals $AE$ , $EI$ , and $IA$ respectively so that $B$ meets $L$ , $D$ meets $F$ , and $H$ meets $J$ , forming a truncated pyramid with $\triangle AEI$ as its base.

If the height of the truncated pyramid is $\frac{\sqrt{a}}{b}$ , where both $a$ and $b$ are square free positive integers, find $a + b$ .