Dodecagon Resistance
You have a dodecagon, and all the vertices are connected to all the other vertices via 3 0 0 Ω resistors (lines below show where the resistors connect):
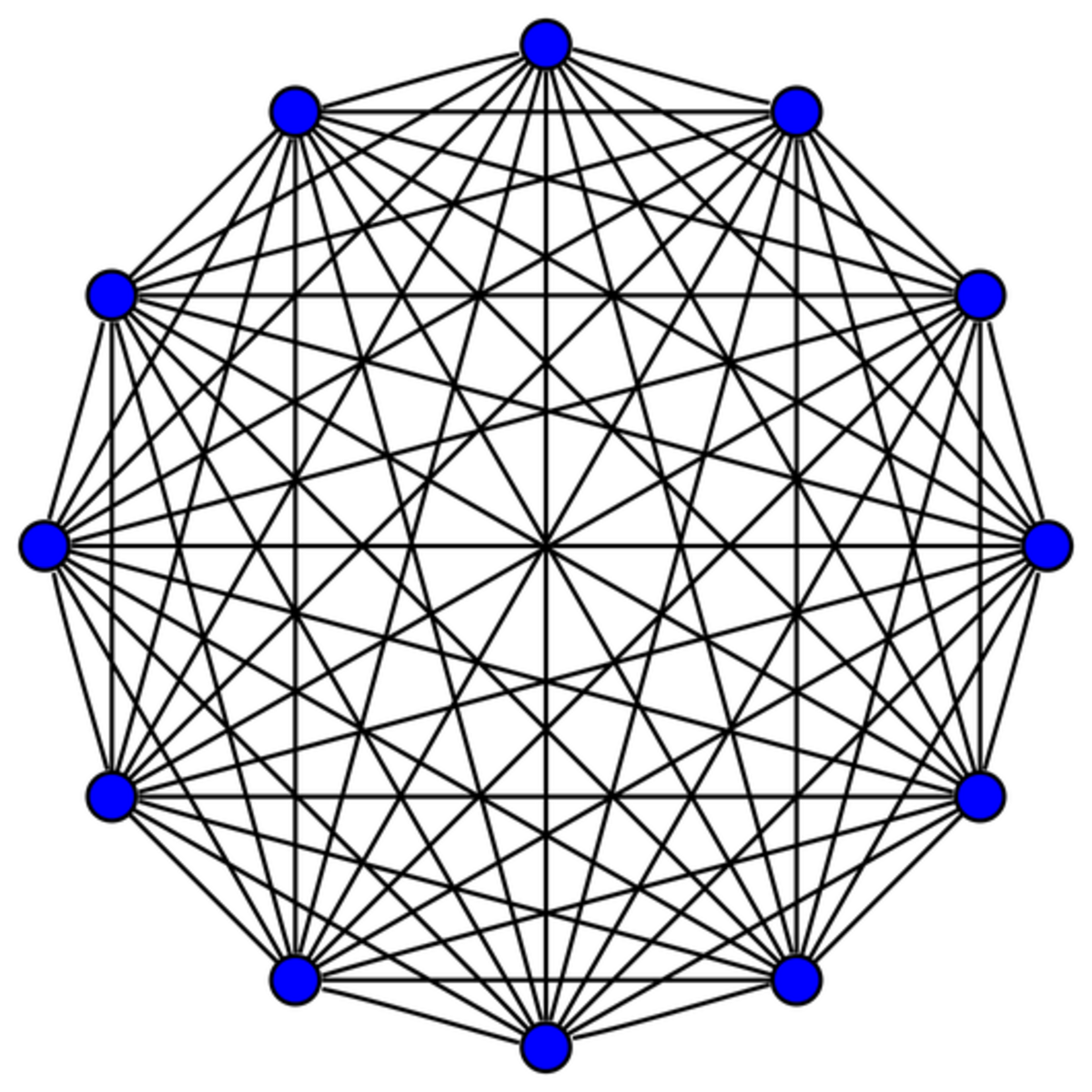
What is the effective resistance between any two vertices in ohms?
Image credit: rosalind.info
The answer is 50.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Didn't quite get it
There. I've updated the solution to add a bit of clarity. Make sense?
- Pick any two nodes, and mark them as A and B.
- Apply 1 V to node A and ground node B.
-
Remove from the network all the resistors which are not connected to A or B. You should get the following circuit:
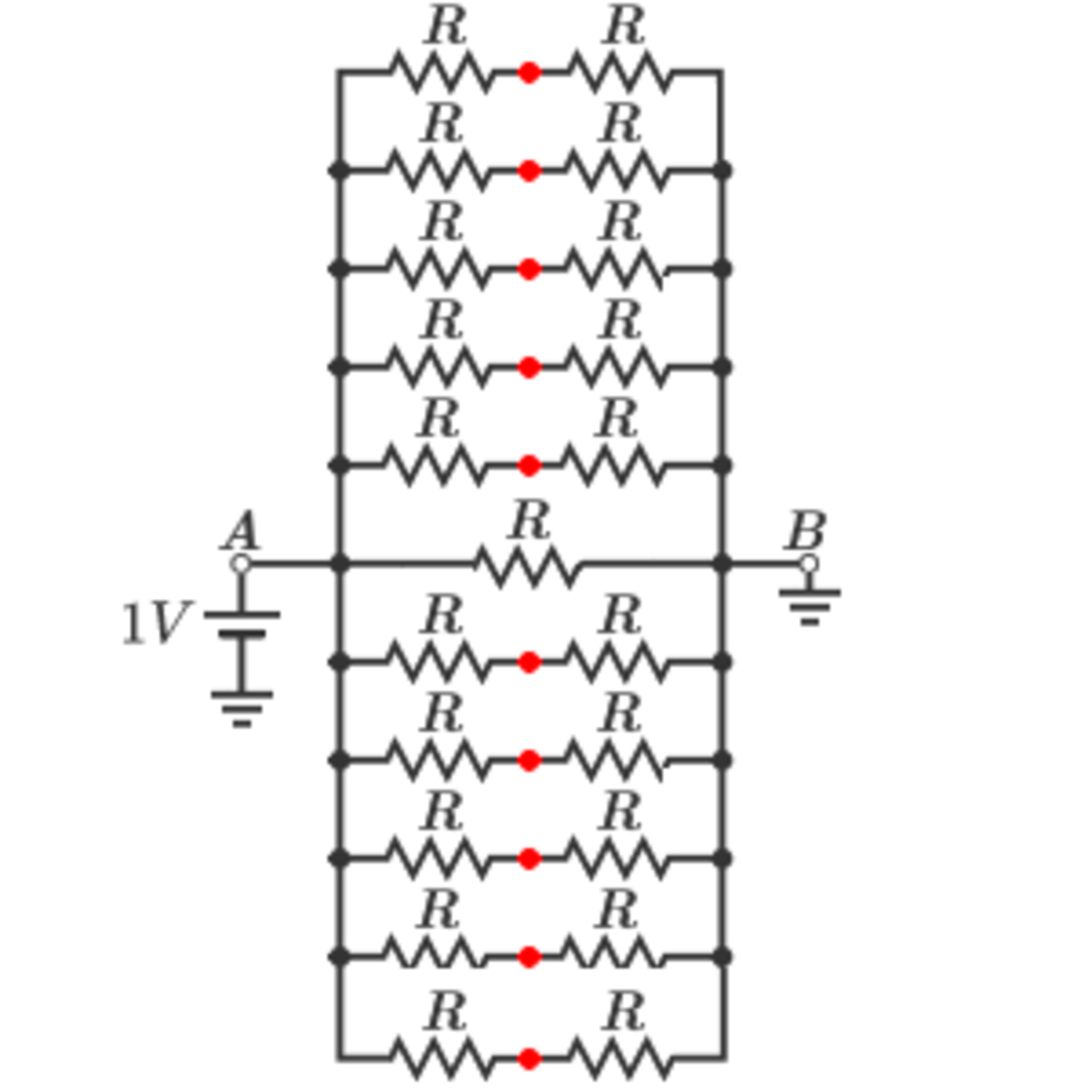
- Resistors you've just removed were previously connected between any two of the red points. It can easily be calculated that the potential of each of the red nodes is 0 . 5 V , meaning that the voltage between any two of the red points is 0 V .
- Try putting all the resistors you've removed back in their place. You will find that each time you connect a resistor back in the circuit, it will end up being connected between equipotential points, which means that no current will flow through it. It turns out that all the previously removed resistors have no impact on the equivalent resistance between A and B, and so it follows that the resistance of the dodecagon network is actually equivalent to the one of the network in the picture I posted here. So, the total resistance is:
R t o t 1 = 1 0 × 2 R 1 + R 1 = 2 R 1 2 = R 6 → R t o t = 6 R = 5 0 Ω
Using exactly the same procedure, this can be generalized for networks represented as regular polygons with n sides, where the total resistance between any two selected vertices is:
R t o t = n 2 R
If you apply 1 V to one node and ground another node, then by symmetry, all the remaining nodes will be at 0 . 5 V. So the total current going out through the grounded node will be 0 . 5 times the number of nodes that are at 0 . 5 V added to 1 times the node to which 1 V was applied. So I = ( 1 0 ∗ 0 . 5 + 1 ∗ 1 ) / 3 0 0 = 1 / 5 0 . So, the effective resistance will be: R e = 5 0 ohms