Dodecalendar
A dodecahedron has 12 pentagonal faces, and companies have used them to create dodecahedral calendars.
Is it possible to place the months of the dodecahedral calendar such that consecutive months are placed on adjacent faces?
Note: This would allow us to roll the calendar model along an edge from one month to the next. The connection between adjacent months begins with Jan-Feb and ends with Dec-Jan.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Moderator note:
For visualizing, it is easier to use the graph where faces are represented by a vertex, and neighboring faces are represented by an edge connecting the vertices.
We get the graph on the right, which is an aerial view with the bottom face represented by the vertex in the lower right.
The problem then is to label the vertices with 1-12 such that consecutive numbers are connected by an edge.
That's a very nice way to visualize it! Actually, I was inspired to post this problem because somebody actually showed me such a net on paper.
Log in to reply
It's a cool problem, I need such a die!;) How many unique paths are there?
With all due respect, Challenge Master, I find Dan's picture more useful. The graph is mathematically correct but verifying that fact isn't as visually immediate.
Relevant wiki: Hamiltonian Path
Dodecahedron can be thought of as a graph with 1 2 vertices of degree 5 .
Since, every platonic solid considered as graph where faces are vertices, has a hamiltonian cycle, dodecahedron must have a hamiltonian cycle.
Now we just start at any vertex and label it January and move to next vertex in the cycle and label it February , and by continuing in the same fashion, we will eventually have labeled the graph in a way which satisfies the condition.
Hence, the answer is Yes .
Notice that it is the existence of a hamiltonian circuit on the (dual) icosahedron that allows you to solve the problem this way. I think your solution would be clearer if you made this more explicit.
Log in to reply
I agree. Plus, this solution does not really tell why every solid does have such a cycle. It merely restates the problem in a new language.
There is a whole patent to it, a patent of 1956. http://www.google.co.in/patents/US2797512
Nice find. Math does have real world uses (who knew? lol).
If you read the details of the patent, it says
Another object of the invention is to provide a dodecahedron calendar in which the first six months of the year appear on the upper half of the dodecahedron and the latter six months on the lower half of the dodecahedron, whereby dates for the first six months may be read without turning the calendar over and dates for the last six months may likewise be read without turning the calendar over when the position of the calendar has been changed so that the lower half with dates for the latter half of the year is uppermost. Thus it is necessary to turn the calendar over only once during the year.
However, the question requires December to link to January directly.
In that patent, the first and last month of the year are NOT adjacent.
First, draw lines connecting the center of adjacent faces of a regular dodecahedron, which will be the graph of the vertices and edges of an regular icosahedron, the dual of a regular dodecahedron. Then find one of the many looped paths possible.
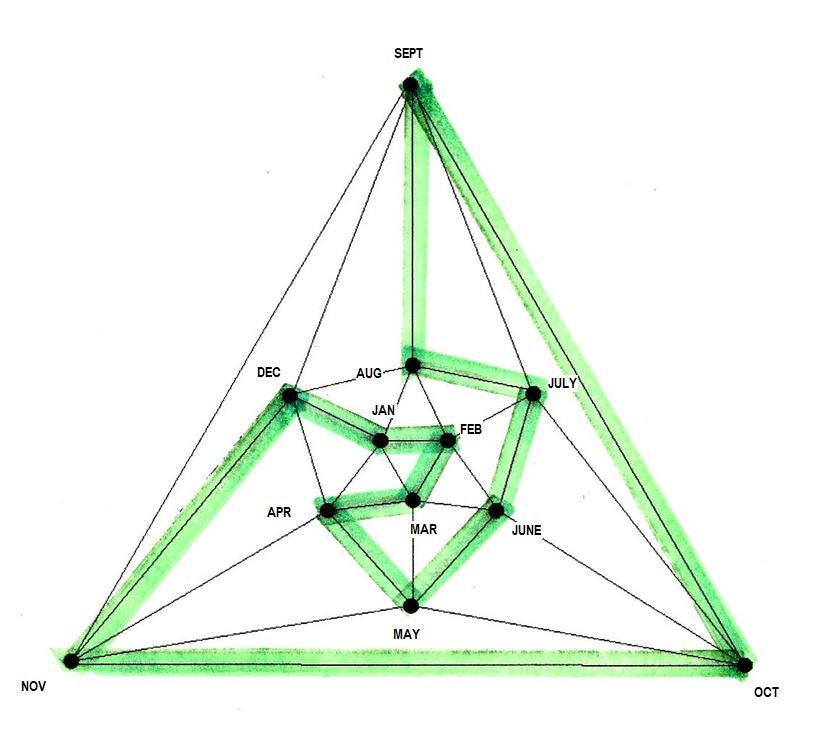 The cluster of 6 vertices near the center could be used for the first six months of the year, using the top half of the dodecahedron, and then the remaining 6 vertices could be used for the second six months, using the bottom half of the dodecahedron, for example.
The cluster of 6 vertices near the center could be used for the first six months of the year, using the top half of the dodecahedron, and then the remaining 6 vertices could be used for the second six months, using the bottom half of the dodecahedron, for example.
As this is part of the Basic quiz, and proving that there is no solution would probably be a very difficult problem in topology, I concluded that the answer is yes.
Sometimes proving that a solution is not that hard. Have you heard of the seven bridges problem?
If we consider the net for a dodecahedron, the visualisation becomes trivial (matching edges are colour coded).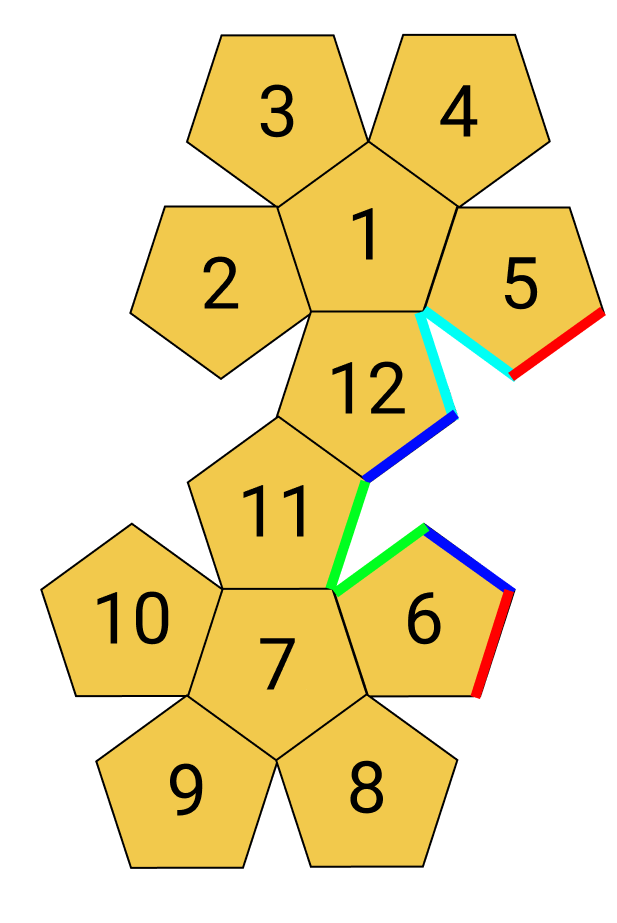 Numbering the months from 1 to 12, the diagram shows one possible path.
Numbering the months from 1 to 12, the diagram shows one possible path.