Does Rotation Help?

Geometry Level 1

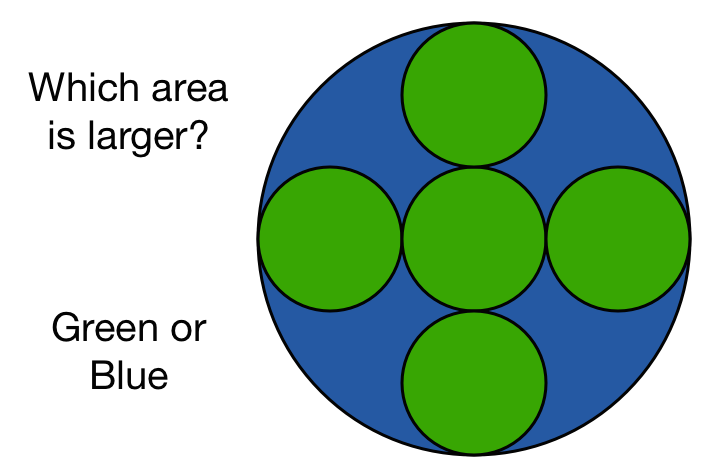
The above diagram shows 5 equal circles arranged in such a way that their centres form a cross ( $+$ ). A large circle is then circumscribed these smaller circles such that it touches all 4 outer circles.

Which of the following has a larger area?

The green region, or the blue region?

The green region The blue region They have the same area

2 solutions

Sravanth C.
Apr 16, 2016

Relevant wiki: Circles - Area

Observe that the vertical diameter of the larger circle intersects the diameters of the $3$ smaller circles. Let us say the radius of the smaller circle is $r$ , hence the radius of the larger circle would be $3r$ . Therefore:

$\begin{aligned} \text{ar(of 5 small circles)}&=5\times (\pi r^2) \\ &=5\pi r^2 \end{aligned}$

$\begin{aligned} \text{ar(of large circle)}&=\pi(3r)^2\\ &=9\pi r^2 \end{aligned}$

$\begin{aligned} \therefore\text{ar(of the region outside the 5 small circles but inside the large circle)}&=9\pi r^2-5\pi r^2\\ &=4\pi r^2 \end{aligned}$

Thus it is clear that the area of the $5$ small circles $=5\pi r^2$ is greater than the area of the region outside the $5$ small circles but inside the large circle $=4\pi r^2$

Maher Farag
May 3, 2016

Thank you for your solution! It's not entirely immediate to know which region has a larger area simply by looking at the picture alone.

Chung Kevin - 5 years, 1 month ago

Does Rotation Help?

2 solutions

0 pending reports