Does the book hold on the wall?
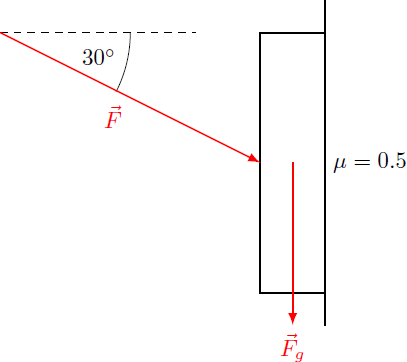
A book of mass M is pressed against the wall by an external force F , which according to the sketch is inclined downwards by an angle of 30 degrees. The coefficient of friction between the book and the wall is μ = 0 . 5 .
Does the book hold on the wall?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The force F can be divided into tangential and normal components: F = F ∥ + F ⊥ = − F sin ( 3 0 ∘ ) e z + F cos ( 3 0 ∘ ) e x The normal component of the force determines the maximal frictional force: F f ≤ μ ∣ F ⊥ ∣ Together with gravitation, a net force results in the vertical direction to ( F g + F + F f ) ⋅ e z ≤ − M g − F sin ( 3 0 ∘ ) + μ F cos ( 3 0 ∘ ) = − M g − 2 1 F + 2 1 2 3 F = − M g − 4 2 − 3 F < 0 Since the total force is always negative, the book fall towards regardless of the strength of the force F .
Let us first look at what happens if the weight is zero, F g = 0 . The normal force (that pushes the book to the wall) is N = F cos 3 0 = 0 . 8 6 6 F . The friction force F f ≤ μ N = ( 0 . 5 ) ( 0 . 8 6 6 ) F = 0 . 4 3 3 F has to balance the force parallel to the wall, F sin 3 0 = 0 . 5 F . Since the maximum value of the friction force is 0 . 4 3 3 F , there is no way to have stable equilibrium. Adding the weight destroys the stabilty even more.