Does the complex number $i$ belong to the Mandelbrot set?

The Mandelbrot set is the set of complex numbers $c$ for which the function $f_{c}(z)=z^{2}+c$ does not diverge when iterated from $z=0,$ i.e., for which the sequence $f_{c}(0), f_{c}(f_{c}(0)), f_{c}(f_{c}(0)), etc,$ remains bounded in absolute value. Whether a number in the complex plane lies in the Mandelbrot set or not depends on these two possibilities:

1. When starting with $z_{0} = 0$ and applying the iteration repeatedly, the absolute value of $z_{n}$ remains bounded however large $n$ gets. It's a property of the function that the upper bound never gets larger than $2$ .
2. When starting with $z_{0} = 0$ and applying the iteration repeatedly, the absolute value of $z_{n}$ is unbounded such that for certain iterations the modulus of the value of the function exceeds 2. It so happens that the higher the number of iterations for such a complex number, the higher would be the modulus of the result.

This is best explained by an example. Let us find out whether $1$ belongs to the Mandelbrot set We have: $f_{c}(z)=z^{2}+c$ For the first iteration, we have $z=0$ and $c=1$ Thus $f_{1}(0)=0^{2}+1 = 1$ For the next iteration, we put $z=1$ and $c=1$ Thus $f_{1}(1)=1^{2}+1 = 2$ Next, we have $f_{1}(2)=2^{2}+1 = 5$ Since the modulus of $5$ is $5$ which is greater than $2$ , the number $1$ does not belong to the Mandelbrot Set.

In contrast, when we take the complex number $-1$ : For the first iteration, we have, $f_{-1}(0)=0^{2}+ (-1) = -1,$ modulus of (-1) is 1 Next we have, $f_{-1}(-1)=(-1)^{2}+ (-1) = 0,$ modulus of (0) is 0 For the next iteration we have, $f_{-1}(0)=0^{2}+ (-1) = -1,$ modulus of (-1) is 1 Hence, we keep on alternating between $1$ and $0$ and the values of never exceed 2.

Similarly, we can prove that $0$ lies in the Mandelbrot set.

Can you tell whether $i$ lies in the Mandelbrot set or not?

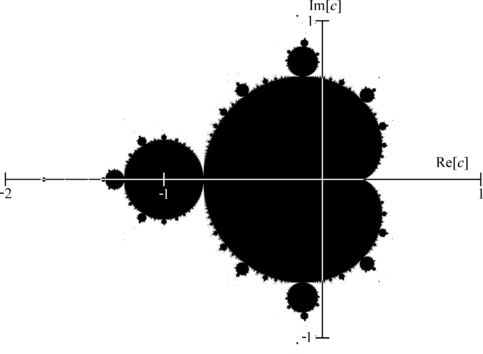
The given image is a mathematician's depiction of the Mandelbrot set M. A point $c$ is colored black if it belongs to the set, and white if not. Re[c] and Im[c] denote the real and imaginary parts of $c$ , respectively.