Dog on a merry go round
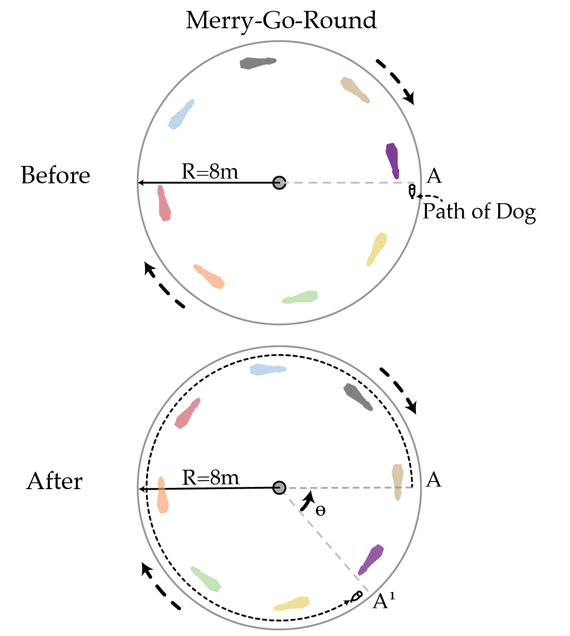
One day after hours at a carnival a dog finds the merry-go-round. The merry-go-round is still, and the dog hops on the merry-go-round and comes face to face with a purple ride-on horse. He then walks around the edge of the merry-go-round at a constant speed to see what else is there. Eventually after some time t he winds up back at the purple horse. By what angle in degrees has the merry-go-round rotated during that time?
Details and assumptions
- The mass of the dog is 20 kg.
- The mass of the merry-go-round is 500 kg.
- The merry-go-round can be modeled as a uniform disk of radius 8 m.
- You may neglect friction.
The answer is 26.67.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
As the dog walks around the merry-go-round, angular momentum is conserved. Therefore, I d ω d + I m ω m = 0 , where I d , I m are the moments of inertia of the dog and merry-go-round and ω d , ω m are the angular velocities. We can use this to solve for ω d in terms of ω m . The total relative angular velocity of the dog with respect to the merry-go-round is ω = ω d + ω m = ( 1 + I m / I d ) ω m . After t seconds the dog has gone around 2 π radians, so we can solve for
ω m = ( 1 + I d I m ) t 2 π .
The distance the merry-go-round has traveled in that time is θ = ω m t , which yields θ = 0 . 4 6 5 r a d i a n s = 2 6 . 6 7 d e g r e e s .
Let angular velocity of dog be ω 1 and that of the ride is ω 2 . By conservation of angular momentum, 1 / 2 × 5 0 0 × 8 2 × ω 2 = 2 0 × 8 2 × ω 1 . So, 2 ω 1 = 2 5 ω 2 . Now relative angular velocity of dog with respect to ride = ω 1 + ω 2 = 2 5 / 2 × ω 2 + ω 2 = 2 7 / 2 × ω 2 . In t sec., dog moves X1 angle with respect to ride and ride moves X2 angle ( with respect to ground). Therefore t = X 1 / ( ω 1 + ω 2 ) = X 2 / ω 2 . Putting X1 = 360 degrees, ω 1 + ω 2 = 2 7 / 2 × ω 2 , we solve for X2=80/3 degrees =26.66 degrees.
Let ω 1 , ω 2 be the angular velocities of the dog and the merry-go-round, respectively. By the conservation of angular momentum, I 1 ω 1 = 2 0 × 8 2 ω 1 = 2 1 5 0 0 × 8 2 ω 2 = I 2 ω 2 . Hence, ω 1 = 1 2 . 5 ω 2 . Let θ 1 be the angular displacement of the dog with respect to the purple horse and θ 2 be the angular displacement of the dog wrt the ground. After some time t= t = ω 1 + ω 2 θ 1 = ω 2 θ 2 , the dog meets the purple ride again, hence θ 1 = 3 6 0 ∘ . Solving the above equation for θ 2 , we get θ 2 = 3 8 0 = 2 6 . 7 ∘ , which is the desired value.
Let angular velocity of dog be (w1) and that of the ride is (w2). By conservation of angular momentum, 1/2 * 500 * 8^2 * (w2) = 20 * 8^2 * (w1) So, 2 (w1)=25 (w2) Now relative angular velocity of dog with respect to ride = (w1)+(w2) =25/2 * (w2)+(w2) = 27/2 * (w2) In t sec., dog moves (X1) angle with respect to ride and ride moves (X2) angle ( with respect to ground.) t = (X1)/((w1)+(w2)) = (X2)/(w2). Putting (X1) = 360 degrees, (w1)+(w2) = 27/2 * (w2), (X2)=80/3 degrees. Therefore the answer is 26.667 degrees.
the angular momentum of the whole system is conserved in the absence of external torque.Here the system(merry go round+dog)is not affected by an external torque.So the angular momentum of the system initially and finally is 0.
Let Wd be angular speed of dog wrt to ground and Wm be angular speed of merry go round wrt to ground. initially there is no rotation therefore the total angular momentum is 0. when the dog starts to go around ,the disk starts to go around in the opposite direction for the angular momentum to be conserved.
therefore Ld+Lm=0 Ld(angular momentum of dog)=Id Wd=M (R^2) Wd=1280 Wd Lm(angular momentum of disk)=Im Wm=0.5 M (R^2) Wd=16000*Wm
Ld+Lm=0
16000Wm=-1280*Wd Wd=-12.5Wm
let them meet after angle 'G'(angle turned by disk) after time t.
therefore (2pi-G)/Wd=G/Wm simplifying we get G=26.667 degrees