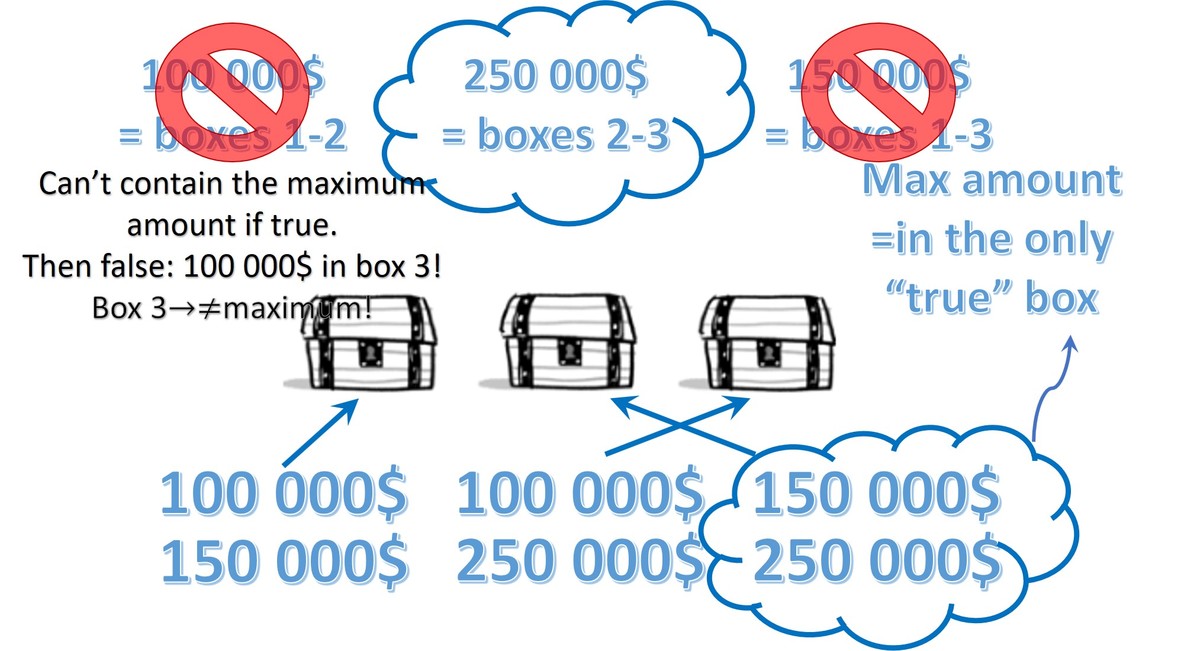
To save some work, I will start off with an educated guess and use the fact that the box with the true statement must contain the largest amount of money. Since $100k+150k=250k$ , a box with $250k$ inside must have the true statement. Furthermore, all boxes include themselves in their statements and thus only if we assume the second boxes' statement to be true, could we save some work. So let's do that.

The boxes' contents can be represented in a table like this:

If we assume the second box's statement to be true, we immediately find that

and reversely, for the second box's statement to be true, it must contain the largest amount of money, meaning $250k+150k$ ,

so that in this case, the only possible configuration becomes

Cross-checking with the fact that statements one and three must now be wrong, we find that this is the desired configuration and thus the answer is $150k+250k+2+1=400003$ .

Note : if,for example,a statement is saying

both $2^{nd}$ and $3^{rd}$ have $100000 in them is $\textcolor{#D61F06}{false}$

It means that (either $2^{nd}$ box OR $3^{rd}$ box) AND $1^{st}$ box(for sure)will have the $100000 envelope .

There are two solutions and I realised the second after answering the question.

1. By Logic

At work

2. By ‘logic‘

Since no box holds two envelopes with the same amount of money, the maximum amount of money has to be $\$250000+\$150000=\$400000$ . Meanwhile, there are only three possibilities of the boxes: 1,2 and 3, i.e. three possible answers $400002,400003$ and $400004$ . Since brilliant system allows us 3 chances, by ‘trial and error’ we get the answer $400003$ .

$\color{#D61F06}\huge \text{I am a GENIUS}$

There are 3 boxes. Each box contains 2 envelopes. Each envelope contains cash - two of them contain $\$250,000$ each, two of them contain $\$150,000$ each and remaining two contain $\$100,000$ each. No box holds envelopes with same amount of money.

These statements tell us that the amounts which can be in various boxes are:

• $\$100,000+\$150,000 = \$250,000$

• $\$100,000+\$250,000 = \$350,000$

• $\$150,000+\$250,000 = \$400,000$

We can infer that the box whose statement is true does not contain any envelope containing $\$100,000,$ because the box with the true statement contains the maximum amount and the maximum amount is obtained by $\$150,000$ and $\$250,000$ . If the statement on box 1 is true, then box 1 can have a maximum amount of $\$350,000$ . Therefore, the statement on box 1 isn't true.

If the statement on box 3 is true, to get the maximum amount in the third box, the values will be as in the table:

But this arrangement contradicts the fact that only one statement is true. So the statement on box 2 should be true and we get the arrangement as

Our answer becomes $2+400000+1 = \boxed{400003}$

Since the maximum amount has to be in the box with the true statement, the latter should assert that it contains the maximum amount. Clearly, any box containing the maximum amount has to contain the amount of 2,50,000 dollars and box 2 asserts that it contains it. So Box 2 is clearly a candidate. Let us check. For it to contain the maximum amount, it should contain an additional amount of 1,50,00 dollars (400,000 in total) while box 3 should contain an additional amount of 100,000 (350,000 in total) . It can be seen that the other statements are false.

We're told that the richest box is the only honest box. Since there's just two copies of each envelope and none of the copies stayed together, each of the box must have different total amount and therefore the richest box may only contain the two distinct top amount of 💰, that is $250k envelope and $150k envelope both for a sum of $400k.

Now that we have cleared that part, moving on to finding the honest box is easy. Honest = richest, so we know that it doesn't have any $100k envelopes inside, therefore one possibility is that this honest box may tell the truth that both other boxes have them ($100k envelopes) inside. After a brief rechecking, Box 1 with mentions of those lowest value envelopes included itself as one of the containers, an obvious lie there and thus, Box 1 is neither honest nor richest, so it must have actually contained that lowest value angpao itself (only honest richest doesn't carry one) and the lie must have lied within the word "both" in "Both, box 1 and box 2...". As of now, we already know that Box 2 doesn't contain the reported envelopes as claimed by the lying Box 1, so Box 2 is our honest richest.

Answer
= 400000 + 2 + 1
= 400003

Since no box holds envelopes with the same amount of money, the boxes will have:

• $400K (max) ($250K + $150K)
• $350K ($250K + $100K)
• $250K (min) ($150K + $100K)

---

The statements can be re-written as:

1) Box 1: Box 1 and Box 2 contain $100K $\Rightarrow$ Box 3 doesn't contain $100K $\Rightarrow$ $\boxed{\text{Box 3 contains \$150K and \$250K}}$

2) Box 2: $\boxed{\text{Box 2 and Box 3 contain \$250K}}$ $\Rightarrow$ Box 1 doesn't contain $250K $\Rightarrow$ Box 1 contains $100K and $150K

3) Box 3: Box 3 and Box 1 contain $150K $\Rightarrow$ Box 2 doesn't contain $150K $\Rightarrow$ $\boxed{\text{Box 2 contains \$100K and \$250K}}$

---

Now, if (1) is true, then Box 3 contains $150K + $250K = $400K. But then, this box does not contain the maximum account, and hence, its statement is false.

If (3) is true, then (2) is false, and Box 2 and Box 3 do not contain $250K. But then, Box 3 cannot contain the maximum amount, and this statement is also false.

If (2) is true, then (3) is false, and Box 2 does contain $150K. According to its own statement, it contains $250K as well.

Hence, (2) is true. And Box 2 contains the maximum amount, $400K.

First of all since there are only 2 envelopes of each ( $\$100000 {,~} \$150000 {~and~} \$ 250000$ ) let's simplify the statements written on the box as follows:

Box1 : Box 3 does NOT contain $\$100000$

Box2 : Box 1 does NOT contain $\$250000$

Box3 : Box 2 does NOT contain $\$150000$

The statement on the box with maximum money is true (value of truth!!!)

According to given condition the three boxes have one of the following combination:

• $\$100000$ and $\$150000$
• $\$100000$ and $\$250000$
• $\$150000$ and $\$250000$

Since there are only three combinations and only three boxes, The box with maximum money (and a true statement on it) will have a total of $\$150000 + \$250000=\$400000$ . Here note that it cannot contain the envelope with $\$100000$ .

Let's assume Statement on Box1 is True . Then it will have the maximum money ( $\$150000{~and~} \$250000$ ) However according to the statement written on it, it should have $\$100000$ . This is contradictory. Hence our assumption is wrong.

So statement on Box1 is False . As the statement is false, it's simplified version is also False . So Box 3 DOES contain $\$100000$ . Hence Box3 cannot contain the maximum amount. As a result the statement on Box3 is also False . As atleast 1 statement needs to be true, $Statement~on~Box2~is~true~and~Box2~contains~the~maximum~value~of~\$400000$ .

$2+400000 + 1 = 400003$ is the answer

If box $2$ has a right statement, box $3$ and box $2$ has $ $250000$ in it. Since we want to maximize the value of money in box $2$ , box $2$ must contain $ $250000$ and $ $150000$ in it. So the answer is $250000+150000+2+1=\boxed{400003}$ .

$If\space statement\space of \space box\space 1 \space is \space true :$ $Box \space 1 \space and \space 2 \space must \space have\space \$ 100,000$ $Since \space only \space \$150,000 \space and \space \$250,000 \space envelope \space are \space left \space and \space no \space box \space have \space the \space same \space envelope$ $therefore box\space 3 \space have \space \$150,000 \space and \space \$250,000 \space envelope$ $\because box\space 2 \space must \space have \space false \space statement \space we \space will \space be \space considering \space \$250,000 \space in \space in\space box\space 1$

$\Rightarrow box\space 1 \space doesn't \space have \space the \space maximum \space amount$ $\therefore there\space is \space a \space contradiction$ $\therefore statement\space on \space box \space 1 \space must \space not \space be \space true \space as \space it \space leads \space to \space contradiction$

---

$If\space statement\space of \space box\space 3 \space is \space true :$ $Box \space 3 \space and \space 1 \space must \space have\space \$ 150,000$ $Since \space only \space \$100,000 \space and \space \$250,000 \space envelope \space are \space left \space and \space no \space box \space have \space the \space same \space envelope$ $therefore box\space 2 \space have \space \$100,000 \space and \space \$250,000 \space envelope$ $\because box\space 2 \space must \space have \space false \space statement \space we \space will \space be \space considering \space \$250,000 \space in \space in\space box\space 1$

$\Rightarrow box\space 3 \space doesn't \space have \space the \space maximum \space amount$ $\therefore there\space is \space a \space contradiction$ $\therefore statement\space on \space box \space 3 \space must \space not \space be \space true \space as \space it \space leads \space to \space contradiction$

---

$If\space statement\space of \space box\space 2 \space is \space true :$ $Box \space 3 \space and \space 2 \space must \space have\space \$ 250,000$ $Since \space only \space \$100,000 \space and \space \$150,000 \space envelope \space are \space left \space and \space no \space box \space have \space the \space same \space envelope$ $therefore box\space 1 \space have \space \$100,000 \space and \space \$150,000 \space envelope$ $\because box\space 3 \space must \space have \space false \space statement \space we \space will \space be \space considering \space \$150,000 \space in \space in\space box\space 2$

$\therefore statement \space on \space box \space 2\space is\space true$ $Answer=400,000+2=400002$

I consider the three cases:

Assume that the statement on box 1 is true:

Boxes 1 and 2 each have $100. Box 3 must have $150 and $250 (in order to have two different amounts, and $100 is not available, as both are already used). Box 3 therefore has more than box 1, so this is not the answer.

Assume that the statement on box 3 is true:

In this case, boxes 1 and 3 each have 150. In order to have the most, box 3 must have $250 also. Both of the $150 envelopes are accounted for (in boxes 1 and 3), therefore box 2 must have $100 and $250. That leave one envelope with $100 to go into box 1. In this case, the statement on box 1 is also true (as boxes 1 and 2 each have $100) and that is a contradiction as we are given that only one statement is true, so this is not the answer.

Assume that the statement on box 2 is true:

Boxes 2 and 3 each have $250. Box 2 also has $150 and therefore has the most. Box 1 must have $100 and $150 (because it must have two different amounts, and neither can be $250, becaue both of the $250 envelopes are already used). That means box 3 must have $100. Box 2 has the most, and all of the conditions are satisfied, so box 2 is the correct answer.

This table follows the statements and their validity, remember, if a statement isn't true, it's just that only one box contains a given amount and not Both . We're further told that there's no box having the two envelopes in it of same value, now the table becomes,

Here we find that only Box 2 can be the one with largest value as only it allows itself to have the largest value when the statement written on it is true.

Thus the answer is $400000+2\red{+1}=\boxed{400003}$

For the sake of simplicity I am assuming 100000 = 10, 150000 = 15 and 250000 = 25.

The maximum amount possible is 25 + 15 = 40. Then this forces the Box with true statement should be either Box 2 or 3. Since then either Box 2 or 3 immediately receive either 15 or 25.

Suppose if generally some Box X states the true statement. Then the way to find what amount is in what box is very simple. Now since Box X states truth go the statement where in it Box X is not mentioned (like Box 1 is not mentioned in Statement 2) now that this statement is false therefore Box X should contain the amount stated in that statement. Now we know what Box X contains (the amount stated in Statement by X and the statement X is not mentioned), similarly we can find the amounts in other boxes.

Therefore the Box 2 is the required Box and the answer is 2 + 400000 + 1 = 400003

Hey @Brilliant Mathematics , can you just check if the logic holds valid for this problem? I'm a bit skeptical. Thanks!