Dominant peg

Classical Mechanics Level 4

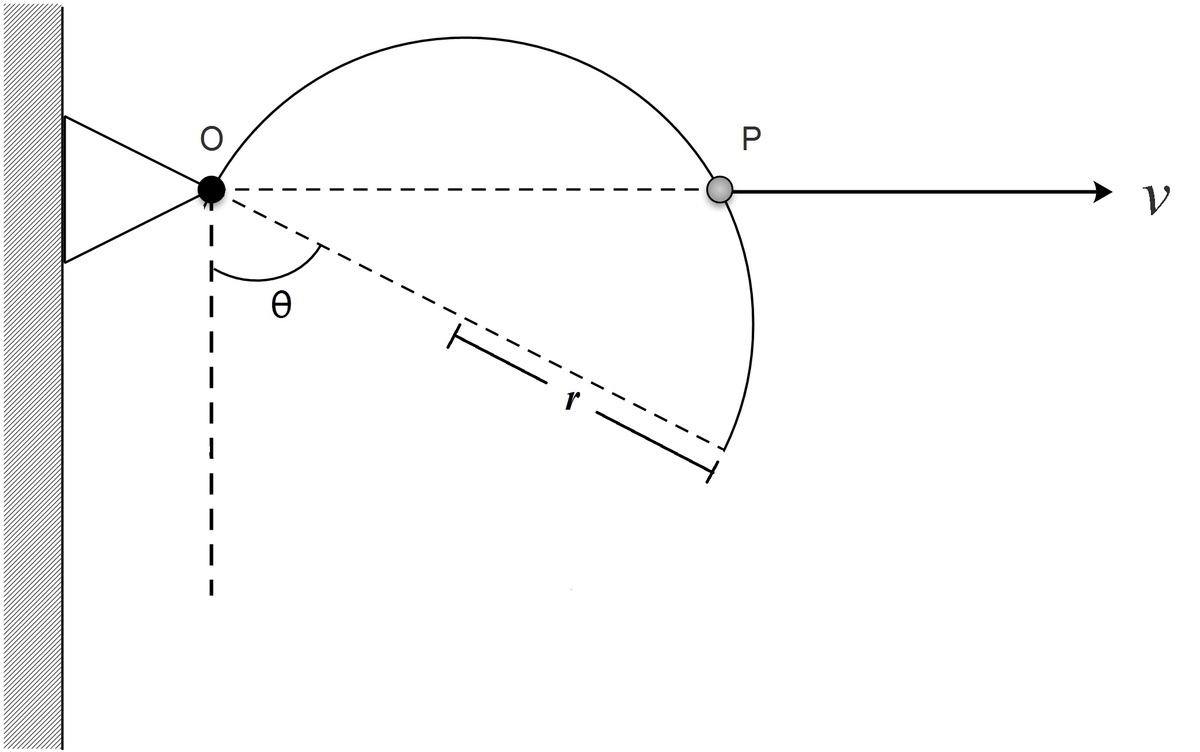
A semicircular wire of radius $r$ is supported in its own vertical plane by a hinge at $O$ and smooth peg $P$ as shown. If peg starts from $O$ and moves with constant speed $v$ along horizontal axis through $O$ . The angular speed of wire at time $t$ is of the form $\frac{m}{n}$ , where $m$ and $n$ are coprime positive integers. Find $\sqrt [ m ]{ n }$ .

Details

$r=5 \text{ m}, v=3 \text{ms}^{-1}, t=2\text{ s}$ .

3 1 6 2

1 solution

Chew-Seong Cheong
Dec 27, 2015

Let $OP = x$ . As $P$ is on the circumference, the angle at $P$ must be a right angle. Then we have:

$\begin{aligned} x & = 2r \cos \left( \frac{\pi}{2} - \theta(t) \right) \\ \Rightarrow vt & = 2r \sin \theta(t) \\ \text{Differentiate both sides:}\quad v & = 2r \cos \theta(t) \space \frac{d\theta}{dt} \\ \Rightarrow \text{Angular speed} \quad \omega(t) & = \frac{d\theta}{dt} = \frac{v}{2r \cos \theta(t)} \\ \text{When } t = 2 \quad \Rightarrow 2v & = 2r \sin \theta(2) \quad \Rightarrow \sin \theta(2) = \frac{v}{r} = \frac{3}{5} \quad \Rightarrow \cos \theta(2) = \frac{4}{5} \\ \Rightarrow \omega (2) & = \frac{3}{10 \times \frac{4}{5}} = \frac{3}{8}\space rads^{-1} \end{aligned}$

$\Rightarrow \sqrt [m]{n} = \sqrt [3]{8} = \boxed{2}$

Thank you for the solution, sir.

Rohit Ner - 5 years, 5 months ago

Dominant peg

1 solution

0 pending reports