Domino Tiling - 5

Probability Level 1

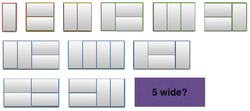
Using 1'' x 2'' dominoes, there's one way to tile a 1'' x 2'' area, 2 ways to tile a 2'' x 2'' area, 3 ways to tile a 3'' x 2'' area, and 5 ways to tile a 4'' x 2'' area.

How many ways are there to tile a 5'' x 2'' area?

5 6 7 8 9

3 solutions

Alan Yan
Aug 10, 2015

This is just a recurrence relation for the Fibonacci Sequence. For a $n \times 2$ region, the number of arrangements is just $F_n$ . This is because you can either end on two horizontal dominoes( $F_{n-2}$ ) or one vertical dominoe ( $F_{n-1}$ ), therefore $F_n = F_{n-1}+F_{n-2}$

Not exactly. The Fibonacci sequence starts with 1, 1. While our sequence starts with 1, 2.

Samuel Godswill - 2 years, 11 months ago

Achille 'Gilles'
Aug 13, 2015

8 ways for 5"x2"

(IIIII, =III, I=II, II=I, III=, ==I, =I=, I==)

13 ways for 6"x2"

(IIIIII, =IIII, I=III, II=II, III=I, IIIII=, ==II, =I=I, =II=, I==I, I=I=, II==, ====)

21 ways for 7"x2"

(IIIIIII, =IIIII, I=IIII, II=III, III=II, IIII=I, IIIII=, ==III , =I=II , =II=I , =III=, I==II , I=I=I , I=II= , II==I , II=I= , III== , ===I , ==I=, =I==, I===)

1, 2, 3, 5, 8, 13, 21... it look like the Fibonacci sequence, isn’t it?

Brindha Lekshmisaran
Feb 22, 2021

Fibonacci Series.

1 + 2 = 3

2 + 3 = 5

3 + 5 = 8

Domino Tiling - 5

3 solutions

0 pending reports