Don't be dense now
Computer Science
Level
4
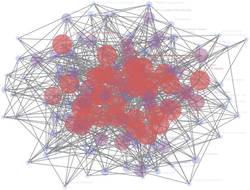 What is the density of the following simple undirected
graph
?
What is the density of the following simple undirected
graph
?
Details and Assumptions:
- The given link is the adjacency matrix representation of the graph.
- The density of a simple undirected graph having vertices and edges is .
The answer is 0.2490.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The density is defined as v ( v − 1 ) 2 e where v , e are the number of vertices and edges respectively. By simply doing a text replacement, we can count that there are 1890
0s and 6101s.1s means there are 305 edges, so e = 3 0 5 .0s and 6101s mean 2500 numbers in total. Since this is exactly the number of entries of a square matrix (the adjacency matrix is always square), the matrix is 5 0 × 5 0 . Thus, there are 50 vertices in total, or v = 5 0 .Plugging the values in gives the answer immediately, 2 4 5 6 1 ≈ 0 . 2 4 8 9 .
This is not even a graph theory problem, just a string problem.