Don't be greedy
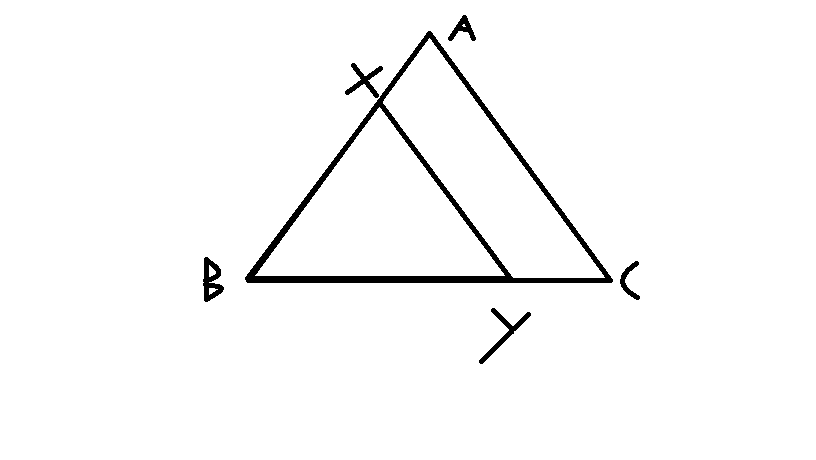
In figure above, the line segment X Y is parallel to side A C of triangle A B C into two parts of equal areas.
Find the ratio A X : A B .
The answer is 0.293.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Same way exactly
Did it in my mind! (Besides the calculation part)😜
Same way !! But nice solution . Upvoted
First, let's find the area of a general equilateral triangle given the base length b . We know that all angles in an equilateral triangle are 3 π , so, assuming we have the triangle centered on the origin, the height must be b sin ( 3 π ) = 2 b 3 . As we are only interested in the ratio between A X and A B , we can let b = 1 WLOG. Applying the formula for area of a triangle, we then have a ( Δ A B C ) = 2 ( 2 b ( 3 ) ) ( b ) = 4 b 2 3 Since b = 1 , a ( Δ A B C ) = 4 3 . We are given that a ( Δ A X Y ) = 2 a ( Δ A B C ) = 8 3 . Using the equation above, 8 3 = 4 b 2 3 2 3 = b 2 3 2 1 = b 2 b = 2 2
Therefore, B X = B Y = 2 2 . It can be seen that A X = 1 − B X = 1 − 2 2 . The desired ratio is then 1 1 − 2 2 = 1 − 2 2
Moderator note:
You made the unnecessary assumption that we have an equilateral triangle.
How can we find the ratio for a general triangle?
a r e a ( X B Y ) 2 ⋅ a r e a ( X B Y ) a r e a ( X B Y ) a r e a ( A B C ) ∴ B X A B A B A X ⇒ 1 − 0 . 7 0 7 1 = a r e a ( A X Y C ) = a r e a ( A B C ) = 2 = 2 = A B A B − B X = 1 − 2 1 = 0 . 2 9 2 8 ∼ 0 . 2 9 3