Don't be under pressure while finding the pressure
IF WE HAVE A HYPOTHETICAL SPHERE OF MASS DENSITY ρ (HERE ρ IS A POSITIVE CONSTANT) AND IF THE RADIUS IS 'R' THEN ASSUMING THAT OUR SPHERE IS IN VACUUM FIND THE PRESSURE AT THE CENTRE OF THE SPHERE.(ASSUME THAT OUT OF THE FOR FUNDAMENTAL FORCES ONLY GRAVITY IS HELPING IN DEVELOPING PRESSURE AT THE CENTRE AND ALSO HERE G IS UNIVERSAL GRAVITATIONAL CONSTANT.AND ALSO ASSUME THAT NEWTONIAN GRAVITY IS SUFFICIENT TO SOLVE THIS PROBLEM AND WE DON'T REQUIRE GENERAL RELATIVITY AS GRAVITATIONAL FIELD STRENGTH ARE NOT VERY LARGE.)
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
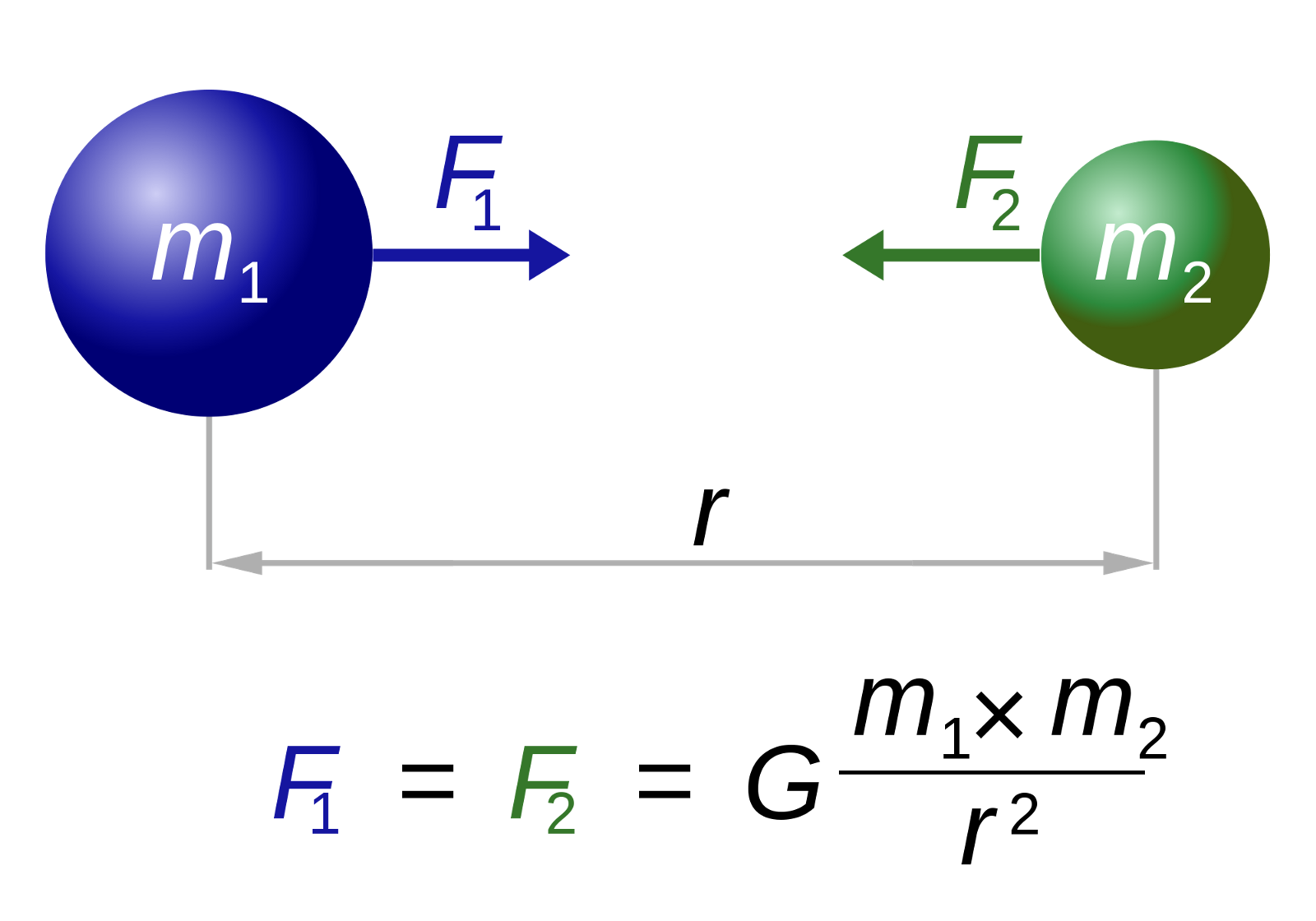
For the given sphere assume a small δA element (area element) on the sphere at some radius r. Now if we'll move from r to r+δr then we'll have a small volume element δV=δA*δr. Now as the mass density is uniform and we know its volume so we can get its mass by definition by this eq》 δm =ρδV. Now we can find the force on this small element due to the rest sphere using either Newtons shell law or Gauss law . We'll get that gravitational field of the part of sphere inside radius r is only effectively applying force. Now by for that small δm element there will be p+δp pressure at r and p pressure at r+δr. Now at equilibrium it is not moving so the force of gravity exactly balances the force due to this pressure difference. Now after remembering that δp δA=δF and then using intergration we'll get the answer.