Don't fall in
A sinkhole begins to open up in a deserted country. In the first year, the sinkhole is a 1 m square, and every year afterwards it grows an additional 1 m square from each of its outer edges.
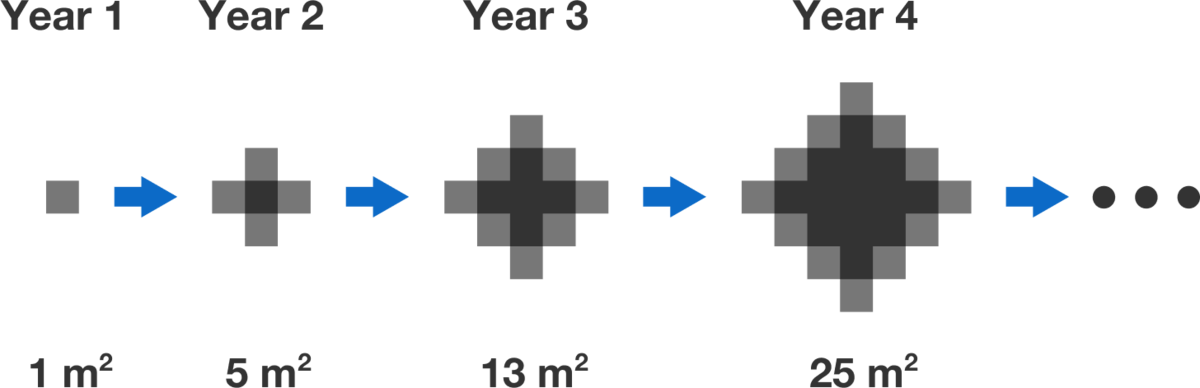
Steve notices the following pattern with the sinkhole area: 0 2 + 1 2 1 2 + 2 2 2 2 + 3 2 3 2 + 4 2 = 1 = 5 = 1 3 = 2 5 . Is the sinkhole area always the sum of the squares of two consecutive integers?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
 By separating the sinkhole into a pattern of alternating colours, we can see each pattern is made of squares in a square formation, with the number of red squares equal to the year squared and the number of blue squares the year minus 1 squared.
By separating the sinkhole into a pattern of alternating colours, we can see each pattern is made of squares in a square formation, with the number of red squares equal to the year squared and the number of blue squares the year minus 1 squared.
Nice and very intuitive solution! It's great that it proofs the fact for all sinkhole sizes at once, no induction is needed.
Nice solution.
I think the digits are consecutive because the pattern repeats in 1 2,2 3,3 4,4 5..... I think I could have also tried to re draw the sinkhole as it shows in the diagram. I would rat this problem a 1 because it was very easy. I felt confident while solving it and it was kind of fun.
Since the sinkhole starts with 1 unit and its width grows by 2 units every year, the sinkhole is 2 n − 1 units across for year n .
When the year n is odd, the sinkhole can be partitioned by its center n x n square, leaving 4 staircase shapes left that have a base of n − 2 and a height of 2 1 ( n − 1 ) that can be rearranged into a second ( n − 1 ) x ( n − 1 ) square, as shown below.
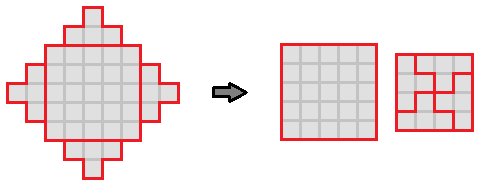
When the year n is even, the sinkhole can be partitioned by its center ( n − 1 ) x ( n − 1 ) square, leaving 4 staircase shapes left that have a base of n − 1 and a height of 2 1 n that can be rearranged into a second n x n square, as shown below.
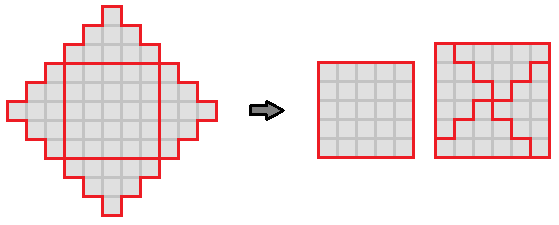
Either way, the sinkhole area for year n is always ( n − 1 ) 2 + n 2 , the sum of the squares of two consecutive integers.
Wow, brilliant explanation 👌🏼
Because this is in a country we can assume it on Earth. This means that the sink hole growth is bounded by size so it cannot grow infinitely. So at some point it will stop growing at that rate.
Let A n be the area of the sinkhole in year n , where n ≥ 1 . We will prove by induction that A n = ( n − 1 ) 2 + n 2 . The base case, n = 1 , is A 1 = 1 = 0 2 + 1 2 . Now, assume that the formula holds for n = k . Note that after year k , the sinkhole grows by an additional 4 k square meters, since each outer edge (northeast, northwest, southeast, and southwest) has k unit squares. Thus, we have
A k + 1 = A k + 4 k = ( k − 1 ) 2 + k 2 + 4 k = k 2 − 2 k + 1 + k 2 + 4 k = k 2 + 2 k + 1 + k 2 = k 2 + ( k + 1 ) 2 .
This completes our inductive step, so we conclude that yes , the area of the sinkhole is always the sum of two consecutive perfect squares.
I didn’t think zero was an integer so I got this wrong
I love this solution
数学归纳法,很不错的解决方法
Why are you allowed to assume that after year k, the sinkhole grows by 4k square meters? What proof is there to show that this is true for all cases?
We will prove this statement true through induction. Let the area of the sinkhole on year y be S y . We have a few base cases given, so we must prove that the area will be a sum of two consecutive squares for all years greater than 4 .
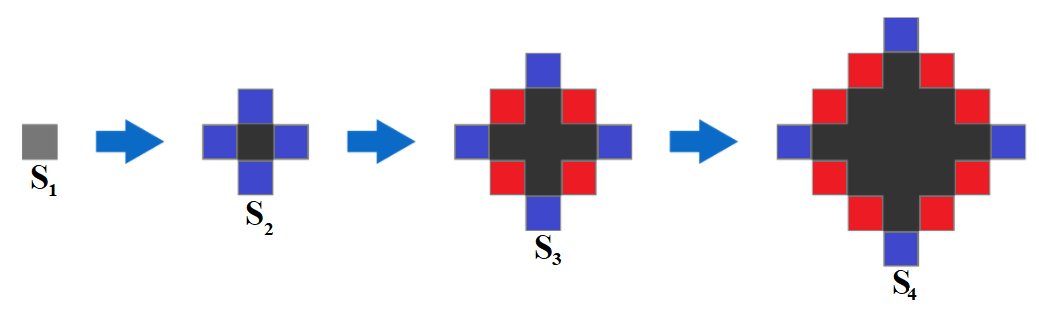
Each year, the sinkhole retains its area from the previous year (in black) but also grows additional squares. The sinkhole always grows 4 blue squares each year, but the number of red squares it grows increases by 4 each year. Because of this, we have the following recursive relationship:
S 1 = 1 S y = S y − 1 + 4 + 4 ( y − 2 ) = S y − 1 + 4 y − 4 , y > 1
Now assume that on some year k , S k = ( k − 1 ) 2 + k 2 .
S k + 1 = S k + 4 ( k + 1 ) − 4 = ( k − 1 ) 2 + k 2 + 4 k = 2 k 2 + 2 k + 1 = k 2 + ( k 2 + 2 k + 1 ) = k 2 + ( k + 1 ) 2
Therefore, the area of the sinkhole on any given year is the sum of two consecutive perfect squares.
Did the same way!!!
The area of the sinkhole for year n may be expressed as A n = 1 + k = 1 ∑ n 4 ( k − 1 ) = 1 + 4 k = 1 ∑ n ( k − 1 ) = 1 + 4 2 n ( n − 1 ) = 1 + 2 n ( n − 1 ) = 1 + 2 n 2 − 2 n = ( n − 1 ) 2 n 2 − 2 n + 1 + n 2 = ( n − 1 ) 2 + n 2 □
If we consider the number of squares in each "column" of the sinkhole we see that they will always be odd numbers, as they begin with 1 and increase by a multiple of 2 each time: 1, 3, 5, 7 etc.
Consequently, reading across the sinkhole and adding up the squares in each column, we find they are composed of sequences of odd numbers, e.g. Year 3 is 1 3 5 3 1. They are also symmetrical, with the numbers on either side of the middle column being the same. Consequently we can consider them to be made of two sequences with n and n+1 odd numbers, e.g. 1 3 5 and 1 3 in the case of Year 3.
As the first n odd numbers sums to n^2, this means that the sinkholes will always be composed of n^2 + (n+1)^2 squares
very reasonable!!!!
The annual increase increases by 4 units. Therefore the area is a quadratic function of time, with leading coefficient 2 1 ⋅ 4 : A n = 2 n 2 + b n + c . WIth A 1 = 1 and A 2 = 5 , it is easy to see that b = − 2 and c = 1 . Now A n = 2 n 2 − 2 n + 1 = ( n 2 − 2 n + 1 ) + n 2 = ( n − 1 ) 2 + n 2 . Yes , the area is always the sum of the squares of two consecutive integers.
please!!! can you explain "the annual increase increases by 4" & also the quadratic function???
Log in to reply
I observed that the growth every year has the shape of the outline of a diamond. The side of that diamond grows by one every step; therefore, its perimeter grows by 4 every step.
In a case like this, it is useful to think about first, second, etc. differences . For instance, if a sequence is linear, its first differences are constant and it second differences are zero: 2 3 5 0 3 8 0 3 1 3 If a sequence is quadratic, its first differences are linear and its second differences are constant, equal to twice the quadratic coefficient: 1 3 4 2 5 9 2 7 1 6
For the sinkhole, the differences are 1 4 5 4 8 1 3 4 1 2 2 5 4 1 6 4 1
By considering the first example you can notice the following pattern for f(n) modelling its area:
f ( 1 ) = 1 + 0 ⋅ 4 , f ( 2 ) = 1 + 1 ⋅ 4 , f ( 3 ) = 1 + 3 ⋅ 4 , f ( 4 ) = 1 + 6 ⋅ 4 , f ( 5 ) = 1 + 10 ⋅ 4 .
So we can deduce, that f ( n ) = 1 + ( 2 n ) ⋅ 4 = 1 + 2 ! ( n − 2 ) ! n ! ⋅ 4 = 1 + 2 n ( n − 1 ) = 2 n 2 − 2 n + 1 .
The pattern which is suggested in the question is: f ( n ) = ( n − 1 ) 2 + n 2 . By multiplying that out, we see, that they are indeed equivalent.
Note that the sum of the first n odd integers is always n 2 . The top half with the middle has an area equal to the sum of the first n odd integers if you add up all the row lengths, where n is the year number. So, that area is n 2 . Similarly, the bottom half has an area equal to the sum of the first n − 1 odd integers, which is equal to ( n − 1 ) 2 . So, the sinkhole area is always the sum of the square of two consecutive integers.
In the initial case when area =1then area=0^2+1^2. Let the induction hold good for n cases.Now,for n+1 Area of n+1=(n-1)^2+n^2+4n =n^2+1^2-2n+n^2+4n =n^2+1^2+2n+n^2 =n^2+(n+1)^2. Therefore it hold good for n+1 case also Hence, the answer is yes.....
Always 4 squares more to add, not including the first one. So add 4 squares to first one and then 8 squares to the second one and then 12 square to the third one and then 16 to the fourth one and 20 to the fifth one and 24 to the sixth one and till infinity. x= y+4 where "y" is a sum of squares added to each edge.
0^2 + 1^2 = 1
1^2 + 2^2 = 5
2^2 + 3^2 = 13
3^2 + 4^2 = 25
4^4 + 5^2 = 41
1 + 0*4 + 4 = 5
5 + 1*4 + 4 = 13
13 + 2*4 + 4 = 25
25 + 3*4 + 4 = 41
1 + 0(4) = 1
1 + 0(4) + 1(4) = 5
1 + 0(4) + 1(4) + 2(4) = 13
1 + 0(4) + 1(4) + 2(4) + 3(4) = 25
1 + 0(4) + 1(4) + 2(4) + 3(4) + 4(4) = 41
x^2 + (x+1)^2 = 4(sum(0..x)) + 1
x^2 + (x+1)^2 = 4(x*(x+1)/2) + 1
x^2 + (x+1)^2 = 2x*(x+1) + 1
x^2 + (x+1)^2 = 2x^2 + 2x + 1
x^2 + x^2 + 2x + 1 = 2x^2 + 2x + 1
2x^2 + 2x + 1 = 2x^2 + 2x + 1