Dont Fall Off This Ladder!
Geometry
Level
3
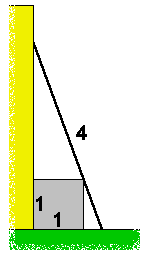A ladder with a length of four meters is placed against a wall. The ladder touches the box of one by one meter, which is standing against the wall.
At what height does the top of the ladder touch the wall?
The answer is 3.76.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Let ABC be the triangle with angle ABC 90 degrees. Let BDEF be the square.
Let x be the length of line segment AD, and let y be the length of line segment CF.
1)Because of the similarity of the triangles ADE and EFC, the following holds: x:1=1:y
So xy=1 . Also x=1/y and y =1/x
2)(x+1)^2 + (y+1)^2 = 4^2
(x^2+2+y^2) + 2x+2y=16
Using xy=1,
(x^2+2xy+y^2) +2x +2y=16
(x+y)^2 +2(x+y)-16 =0.
Solving quadratic equation (x+y) = 3.123
3)x=1/y so x+(1/x)= 3.123
x^2+1= 3.123x
x^2-3.123x+1=0
Solving quadratic equation,
x= 2.76
The height of wall where ladder touches is 2.76 +1= 3.76