Don't find the intersection
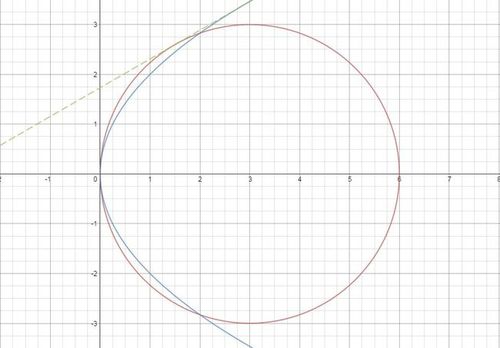
Which of the given equations is the common tangent to the circle ( x − 3 ) 2 + y 2 = 9 and the parabola y 2 = 4 x touching both the conics above the x -axis?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Let m be the slope of the tangent. Equation of tangent to the given parabola with slope as m is y = m x + m 1 and that to the given circle is y = m ( x − 3 ) + 3 1 + m 2 . Equating the constant term in both the equations, we get m = 3 1 . Substituting the value in any of the above two equations, we get 3 y = x + 3
Refer conic sections in JEE to know about the equation of tangents.
I did a bit differently, I found the derivatives of both the functions and equated them to get the slope of my tangent, which equals 1. It is trivial to find an equation with slope of one. And I was done..
1.- La recta es positiva. 2.- El punto donde corta al eje Y es mayor a 1 y menor a 2. 3.- solo una cumple lo anterior
Write in ENGLISH. Please😓😓
Tge only option in which the line is tangentto circle is third one.
Implicitly differentiating the parabola's equation:
2 y d x d y = 4 ⇒ d x d y = x 1
Then taking a point ( a , 2 a ) on the parabola, a tangent is formed:
y − 2 a = a 1 ( x − a )
y = a + a x
Intersecting this with the circle by substitution:
( x − 3 ) 2 + ( a + a x ) 2 = 9
( 1 + a 1 ) x 2 − 4 x + a = 0
For the intersection to be tangential, discriminant is zero. Hence:
1 6 − 4 ( a ) ( 1 + a 1 ) = 0
a = 3
Substituting a = 3 back into the tangent equation:
y = 3 + 3 x
3 y = x + 3