Don't Find Those Nasty roots!
3 cos A + sin A = 2 1
In a triangle A B C , angle A satisfies the above equation. What is triangle A B C ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
this question was asked in an examination
where a calculator is not allowed
I have a solution which is pure which doesn't require any calculations
i will post it tomorrow (due to time constraints - school)
your solution is not wrong but use of calculators is not permitted
so i would like a pure approach
Log in to reply
No, worry. I can change the solution. I was thinking to do so anyway.
Now it's much better
A definitely cannot be in the first quadrant:
If
A
<
3
0
∘
,
3
cos
A
+
sin
A
>
2
3
+
sin
A
>
2
1
If
3
0
∘
≤
A
≤
9
0
∘
,
3
cos
A
+
sin
A
>
3
cos
A
+
2
1
>
2
1
Hence A must fall on the second quadrant, and form an obtuse triangle.
Divide both sides by 2
Now note that lhs is sine of A + 3 π
For lhs to be 0.25, A has to be obtuse as A is positive and arcsin of 0.25 is lesser than 3 π
How can we show (without a calculator) that "arcsin of 0.25 is less than pi/3"?
Log in to reply
Sir I have a solution without use of calculator
I will post it soon
Thats simple
Sine is an increasing function so is arcsin on its principle domain.
Since arcsin 0.5 is is less than pi/3,arcsin 0.25 is also lesser
Your solution is wrong please don't post such solutions
Log in to reply
Your comment is not helpful. Even if Rohit is wrong, you can help him by pointing out his error, otherwise, he will still be making the same mistake because he don't know what went wrong.
when you divide both sides by cos x
RHS becomes 1 /2 cos x
you have not divided both sides
@Neel Khare @Pi Han Goh Yup guys I know I forgot to. Sorry, I am deleting it.
2 ∗ ( 3 / 2 ∗ C o s A + 1 / 2 ∗ S i n A ) = 1 / 2 . ⟹ C o s ( A − 6 0 o ) = 1 / 4 < 1 / 2 = C o s 6 0 o . C o s i s a d e c r e a s i n g f u n c t i o n . S o C o s − 1 1 / 4 > 6 0 o . ∴ C o s ( A − 6 0 o ) > C o s 6 0 o . ⟹ A > 1 2 0 o .
Let cos A = c and sin A = s.
Squaring the equation,
3c^2 + s^2 + 2sc * sqrt(3) = 1/4
= (s^2 + c^2) + 2c^2 + 2sc * sqrt(3)
= 1 + 2c * (c + s * sqrt(3))
2c * (c + s * sqrt(3)) = 1/4 - 1 = -3/4
s = sin A > 0 for any A in a triangle, so RHS could only happen iff c < 0 AND c + s * sqrt(3) > 0
c = cos A < 0 for 90 < A << 180.
==> Triangle ABC has an obtuse angle A.
(earlier solution)
Let cos A = x and sin A = y, and we all know the identity x^2+y^2=1.
Easier to use y than x, so now the equation becomes sqrt(3(1 - y^2)) + y = 1/2
Squaring gets us 3(1 - y^2) = y^2 - y + 1/4 0 = 4y^2 - y - 11/4 = y^2 - y/4 - 11/16 (y - 1/8)^2 = 45/64 y = (1 +- 3 * sqrt(5)) / 8 > 0 for any A of a triangle. y = (1 + 3 * sqrt(5)) / 8 Plugging the above back into the original equation, x = sqrt(3) * (1 - sqrt(5)) / 8 = cos A < 0
==> 90 < A < 180 ==>> Triangle ABC has an obtuse triangle A.
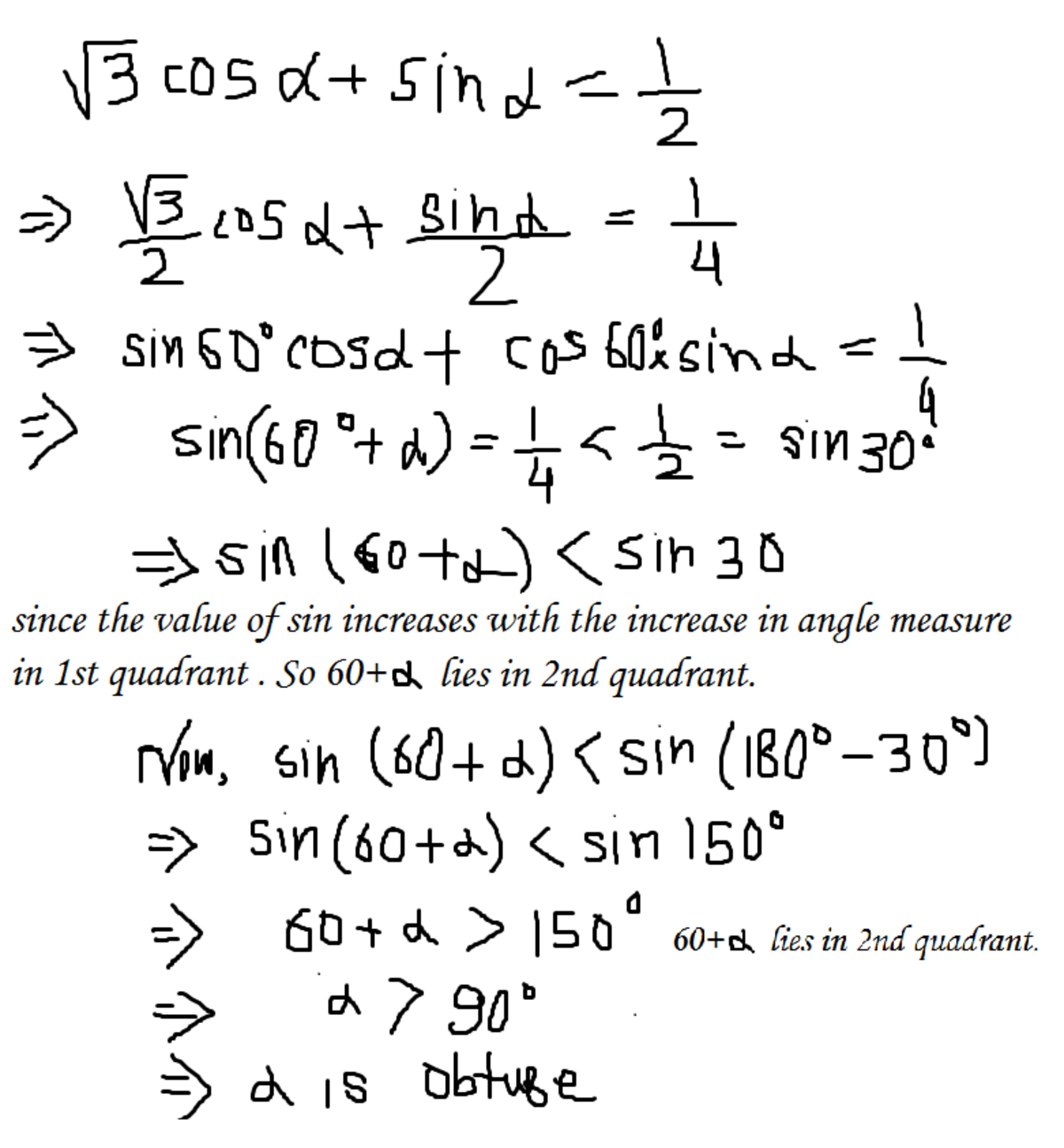
3 cos A + sin A 2 ( 2 3 cos A + 2 1 sin A ) sin ( A + 6 0 ∘ ) A + 6 0 ∘ ⟹ A = 2 1 = 2 1 = 4 1 = sin − 1 4 1 > 1 8 0 ∘ − 3 0 ∘ > 1 8 0 ∘ − 3 0 ∘ − 6 0 ∘ > 9 0 ∘ Obtuse Note that sin − 1 4 1 < 3 0 ∘ For positive A