Don't forget the 3rd law
Newton's third law, that for every action there is an equal and opposite reaction, is essentially a statement about conservation. Without it, we wouldn't have the conservation of energy, momentum, or angular momentum.
We can see this with a simple example: Imagine we have two equal mass objects, A and B, separated by some distance x . A feels an attractive force towards B with some strength F. If we have Newton's third law, then that means that B would be attracted to A by a force of the same strength F . Imagine now we violate this law, and say that A is attracted to B but B is repelled from A (so the forces are in the same direction). Then the AB pair of objects would zoom off to infinity, thereby violating momentum conservation.
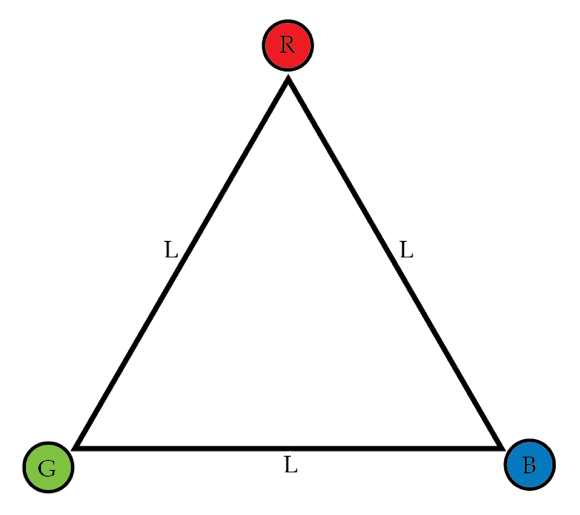
We can play a similar game with angular momentum. I have three objects labelled, (R)ed, (G)reen, and (B)lue each with mass 1 g . The magnitude of the forces between the objects follows an inverse force law, i.e.
∣ F ∣ = d 1 Newtons
where d is the distance between the objects in meters. Such a force, while a little different than you are used to, occurs in nature, for example in 2-d systems. However, I am now going to violate Newton's third law, and give the following rules for how R,G, and B attract or repel:
R is attracted to G, but G is repelled from R.
G is attracted to B, but B is repelled from G.
B is attracted to R, but R is repelled from B.
I arrange my three objects so they are at rest at the tips of an equilateral triangle of side length L meters. At t = 0 I let go of the objects. After 5 seconds , what is the change in the total angular momentum of the system about the centroid of the triangle in kg m 2 / s ?
The answer is 8.66.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Firstly, we must find the effective force acting on three balls, which is given by
3 F = 3 × 2 cos 6 0 ∘ 1 / L = 3 / L N
Now imagine the equilateral triangle is inscribed inside a circle. The radius of this circle is easily determined by the sine rule
sin 3 0 ∘ r = sin 1 2 0 ∘ L m
r = 3 L m
Therefore the effective torque acting on the 3 balls is T = F r = L 3 N × 3 L m = 3 N m = I a
Where I is the moment of inertia, a is the angular acceleration. The moment of inertia of the 3 balls is
I = 3 M r 2 = 3 M × 3 L 2 = 3 M L 2 (M is the mass of one ball)
therefore, a = 3 M L 2 3 N m = 3 M L 2 1 N m
The angular velocity ω after 5 seconds is therefore
ω = a t = 3 M L 2 5 N m s
The angular momentum of the system of 3 particle is therefore
I ω = 3 M L 2 × 3 M L 2 5 N m s = 5 3 k g m 2 / s
Which is actually around 8 . 6 6 k g m 2 / s to 3 significant figures.
At t=0, there are two forces acting on R. One is from R->G while the other is from B->R. Hence their resultant has the direction of B->G and has magnitude 1/L. Since the direction of acceleration is perpendicular to the position vector from the centre of the triangle to R, the distance from R to the centre doesn't change (instantaneously). But the same can be said about G and B. this means that the net effect of the forces is that the triangle rotates as a whole. Hence the force and acceleration on each object is invariant with time.
∣ F ∣ = L 1 ∣ a ∣ = m L 1 ∣ v ∣ = m L t Angular momentum = m v r = m × m L t × L 3 = ( 3 ) t
It is easily seen that the resultant force on each particle is L 1 , parallel to the opposite side of the triangle. However, due to these forces on each particle, the triangle has rotated at the next instant and the direction of the force also changes. However, it always remains parallel to the opposite side, i.e. perpendicular to the the line joining the particle to the centre of mass of the three particles. Hence the only effect of this force is to produce angular acceleration; the size of the triangle does not change. Linear acceleration of each particle is m L 1
Hence angular acceleration about the centre of mass of the three particles is m L 1 . 3 L 1
= m L 2 3
Hence angular velocity after time t
= m L 2 3 t
Total moment of inertia about centre of mass
= 3 ( m ( 3 L ) 2 )
= m L 2
Hence, angular momentum = 3 t
in SI units. Plugging in the values, the answer follows.
By symmetry, the three balls will remain a distance L away from each other as they rotate about the centre of mass. To get the change in angular momentum, simply derive the net torque T on the three balls. Let the radius of the inradius of the triangle be R = 6 3 × L . There are 2 forces acting on each ball, one repelling the ball away from the previous ball, the other attracting the ball towards the next ball. These 2 forces act at the same perpendicular distance R away from the centre. As such, there are 2 × 3 = 6 identical forces acting at a distance R away from the centre. Since each ball is L away from each other, then F = L 1 So the net torque is simply T = 6 × ( R × F ) . Evaluating this statement, we get T = 3 Now, since Torque is change in angular momentum divided by change in time, the change in angular momentum is Δ t × T = 5 3
We know that F = L 1 . Also, using properties of equilateral triangles, we can show that the distance to the center (which is the center of mass) is 3 L .
Since the force is always perpendicular to the radial vector, the torque on each object is just F r = L 1 3 L = 3 1 , so the total torque is τ n e t = 3 3 = 3 .
The angular momentum, then, is just L = ∫ 0 5 τ n e t d t = ∫ 0 5 3 d t = 5 3 ≈ 8 . 6 6 0 2 5 kg m^2/s.
The objects move in a circle of radius L/root3. The force experienced by each of them at the beginning is the resultant of two forces of magnitude 1/L acting at an angle of 120 to each other => the magnitude of the resultant is 1/L which remains constant throughout their motion. The net torque produced by these forces is (L/root3 * 1/L) (for each object) Therefore for all three of them the torque = root3. Now, the integral of the net torque wrt to time ( i.e dt) = change in the angular momentum (the limits here are from 0 to 5 seconds). The change in angular momentum = 5*root3 = 8.660254083... kgm^2/s.
exactly
By symmetry it can be said that the three balls would exhibit similar motion and they would always form an equilateral triangle and the centroid of the triangle would not shift.
Resultant of the repulsive and attractive forces on any ball will be in a direction parallel to the side of the triangle opposite to the ball (this can be seen easily)
Let one of the balls move a small distance dx in this direction. Let us observe the motion from the centroid of the triangle. Let its instantaneous side length be l.
the angle between the direction of motion and of any ball and the line connecting it to the centroid = 6 0 ∘ + 3 0 ∘ = 9 0 ∘
therefore distance of the ball from the centroid = 3 l
new distance = 3 l 2 + d x 2 = 3 l ( d x 2 is too small to be considered)
thus the distance remains virtually constant and the path traced by the balls is circular.
thus the side length remains same as the distance of any vertex from the centroid remains same. therefore l = L at all instants
Hence we come to the conclusion that the balls move in a circular path of radius 3 l the force being tangential and l 1 in magnitude.
therefore we can say that: F= l 1
or d x m × v × d v = l 1
or 3 l × d θ m × v × d v = l 1
or 3 × m × v × d v =d θ
⇒ 3 × m × v 2 = 2 × θ
but v= α × 3 l where α is the angular velocity of the ball abut the centroid of the triangle
⇒ 3 × m × α 2 × 3 l 2 = 2 × θ
α = m L 2 2 3 θ
⇒ d t d θ = m L 2 2 3 θ
Solving the above differential equation
θ = 2 m L 2 3 t 2
⇒ α = m L 2 3 t
angular momentum of one ball= m α l 2 = m L 2 3 t ∗ 3 m L 2 = 3 t = 3 5
total angular momementum = 3 × 3 5 = 5 × 3 =8.66
Let us first consider the force on the red ball. It feels a repulsive force from B and a attractive force towards G, both of magnitude L 1 N . The vertical components of these two forces are equal and opposite while the horizontal component of each is equal to L cos 6 0 ∘ = 2 L 1 N . Since there are two horizontal forces of this magnitude, the net force felt by B has magnitude L 1 N and is horizontal to the left.
Note: Since the applied force is always aligned with the direction of motion, the force directly contributes to the objects speed at all times. Also notice that there is not centripetal force acting on either of the objects. This is because centripetal force describes the motion of an object rotating with constant speed and centripetal force is required to keep the object within the rotational path. This does not apply in this case because there is a constant external force acting in the tangential direction and the speed is not constant, therefore no centripetal force is required.
A similar analysis on the other 2 points yields forces of the same magnitude. The directions are forcing each point to go counterclockwise and as each point moves, the direction of the forces will also move causing the system to spin, and accelerate, in a counterclockwise motion. Since the force on each is L 1 N , we can divide by the mass of 0 . 0 0 1 k g to get acceleration of L 1 0 0 0 s 2 m , which means, if starting from rest, the speed after 5 seconds is L 1 0 0 0 s 2 m ∗ 5 s = L 5 0 0 0 s m .
Now we need to find the radius of rotation. Recall that the circumcenter of an equilateral triangle is intersection of the altitudes. Drawing all three altitudes, we can analyze a subtriangle from the resulting diagram. If we call the 3 outer vertices RGB, the midpoints of these outersegments where the altitudes intersect the sides as ABC, and the circumcenter as D, we can analyze the triangel RDA. This is a right triangle where the leg RA has length L/2 and is opposite a cos 6 0 ∘ angle. The hypotenuse, RD, is the length we are trying to find because it denotes the distance from the point to the circumcenter. Using trigonometry, we find R D = cos 6 0 ∘ R A = 2 L ∗ 3 2 = 3 L
We now need to find the angular momentum L = I ω . Since we have 3 point masses all of mass 0 . 0 0 1 k g , I = 3 ∗ m ∗ r 2 = 3 ∗ 0 . 0 0 1 ∗ ( 3 L ) 2 = 0 . 0 0 3 ∗ 3 L 2 = 0 . 0 0 1 L 2 . ω = r v = L 5 0 0 0 s 2 m ∗ L 3 = L 2 8 6 6 0 s 2 r a d .
We now get L = I ω = 0 . 0 0 1 L 2 ∗ L 2 8 6 6 0 = 8 . 6 6 s k g m 2 .