Don't get trapped
Suppose A B C D is an isosceles trapezoid with bases A B and C D and sides A D and B C such that ∣ C D ∣ > ∣ A B ∣ . Also suppose that ∣ C D ∣ = ∣ A C ∣ and that the altitude of the trapezoid is equal to ∣ A B ∣ .
If ∣ C D ∣ ∣ A B ∣ = b a , where a and b are positive coprime integers, then find a b .
The answer is 243.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
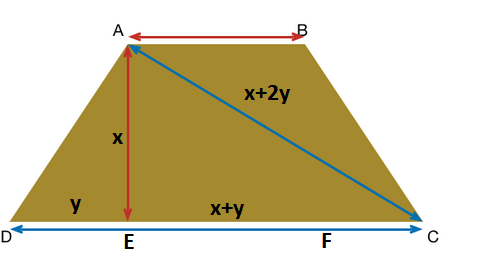 Construct a Line Perpendicular to CD through A and let the point where that line and CD intersect be E. Similarly do the same through B and let the point be F.
Let
A
B
=
x
,
D
E
=
y
.
By the fact that this trapezoid is isoceles DE is equal to FC.
Thus we have
A
B
=
x
,
D
E
=
y
,
E
C
=
x
+
y
,
D
C
=
x
+
2
y
It is stated that CD is equal to AC and since AE is perpendicular to CD we can set up the pythagorean theorem.
A
E
2
+
E
C
2
=
A
C
2
x
2
+
(
x
+
y
)
2
=
(
x
+
2
y
)
2
x
2
+
x
2
+
2
x
y
+
y
2
=
x
2
+
4
x
y
+
4
y
2
Solving this equation:
x
2
−
2
x
y
−
3
y
2
=
0
(
x
−
3
y
)
(
x
+
y
)
=
0
x
=
3
y
,
x
=
−
y
Negative values are extraneous so we have x=3y, AB=3y, and CD=5y.
Thus the ratio of 3:5. And the soultion of 243.
Construct a Line Perpendicular to CD through A and let the point where that line and CD intersect be E. Similarly do the same through B and let the point be F.
Let
A
B
=
x
,
D
E
=
y
.
By the fact that this trapezoid is isoceles DE is equal to FC.
Thus we have
A
B
=
x
,
D
E
=
y
,
E
C
=
x
+
y
,
D
C
=
x
+
2
y
It is stated that CD is equal to AC and since AE is perpendicular to CD we can set up the pythagorean theorem.
A
E
2
+
E
C
2
=
A
C
2
x
2
+
(
x
+
y
)
2
=
(
x
+
2
y
)
2
x
2
+
x
2
+
2
x
y
+
y
2
=
x
2
+
4
x
y
+
4
y
2
Solving this equation:
x
2
−
2
x
y
−
3
y
2
=
0
(
x
−
3
y
)
(
x
+
y
)
=
0
x
=
3
y
,
x
=
−
y
Negative values are extraneous so we have x=3y, AB=3y, and CD=5y.
Thus the ratio of 3:5. And the soultion of 243.
Literally the exact same way I did this. If that's not ESP(N) I don't know what is, Timmy ...
great solution, as i read it the problem didnt seem to be so hard anymore :)
I approached the same way but i am getting AB / CD = 2/3 giving 8.
The working is as follows :
Ab = a
Cd = c
Let c = a + x
A^2 + [[a +x/2]^2= [a+x]^2 [since this is an isosceles trapezoid]
A^2 + a^2 + ax + x^2/4 = a^2 + 2ax + x^2
A^2 + ax + x^2/4 = 2ax + x^2
A^2 = ax + 3x^2/4
Therefore, 3x^2/4 + ax - a^2 = 0, which is a quadratic in x with roots
-a +/- sqrt[a^2+4a^2*3/4]
= [-a + 2a]/2
X = a/2
AB / CD = a/[a+a/2]
= a/[3a/2]
= 2/3, giving 8
Best explained solution so far...awesome!
Amazing solution. Simple, sweet and elegant!
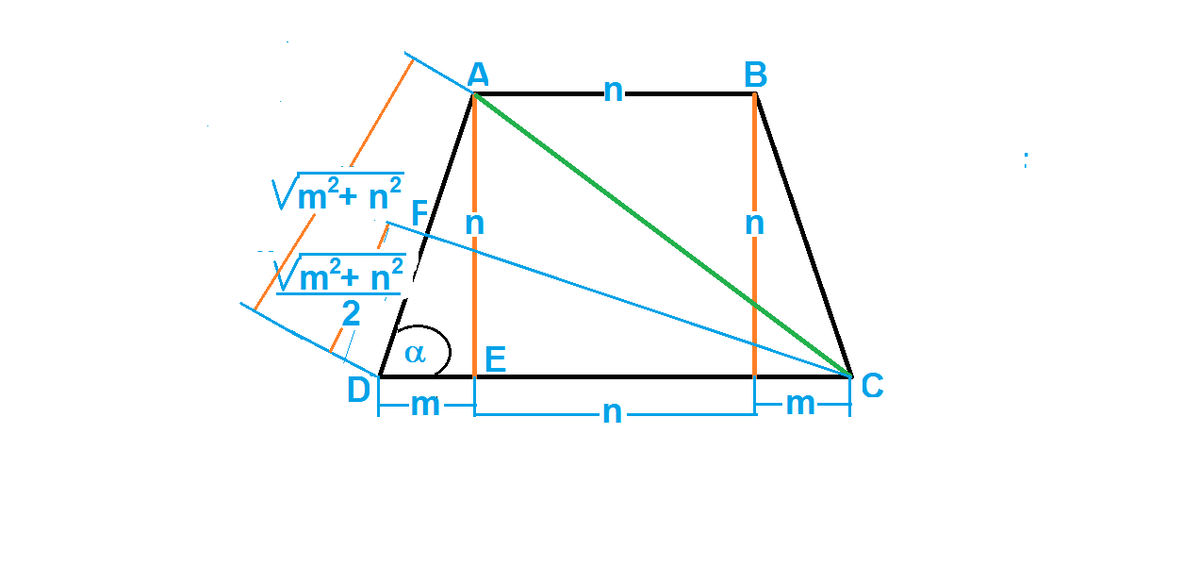 Let n=AB= AE and 2m+n=CD=AC. See figure.
By Pythagoras
A
D
=
m
2
+
n
2
,
h
a
l
f
t
h
e
i
s
o
s
c
e
l
e
s
b
a
s
e
=
2
m
2
+
n
2
.
I
n
r
t
∠
d
△
s
A
D
E
a
n
d
C
D
F
,
m
2
+
n
2
m
=
C
o
s
α
=
2
m
+
n
2
m
2
+
n
2
⟹
4
m
2
+
2
m
n
=
m
2
+
n
2
S
o
l
v
i
n
g
q
u
a
d
r
a
t
i
c
3
m
2
+
2
m
n
−
n
2
=
0
,
m
=
3
n
.
∴
n
=
3
m
.
C
D
A
B
=
2
m
+
n
n
=
2
m
+
3
m
3
m
=
5
3
=
b
a
⟹
a
b
=
3
5
=
2
4
3
Let n=AB= AE and 2m+n=CD=AC. See figure.
By Pythagoras
A
D
=
m
2
+
n
2
,
h
a
l
f
t
h
e
i
s
o
s
c
e
l
e
s
b
a
s
e
=
2
m
2
+
n
2
.
I
n
r
t
∠
d
△
s
A
D
E
a
n
d
C
D
F
,
m
2
+
n
2
m
=
C
o
s
α
=
2
m
+
n
2
m
2
+
n
2
⟹
4
m
2
+
2
m
n
=
m
2
+
n
2
S
o
l
v
i
n
g
q
u
a
d
r
a
t
i
c
3
m
2
+
2
m
n
−
n
2
=
0
,
m
=
3
n
.
∴
n
=
3
m
.
C
D
A
B
=
2
m
+
n
n
=
2
m
+
3
m
3
m
=
5
3
=
b
a
⟹
a
b
=
3
5
=
2
4
3
Nice solution. I like how the three solutions posted so far each have their own twist. :)
Log in to reply
Thank you. Since I am not familiar with higher maths I solve from the basic maths.
i too did the same way...its probably the most simplest method applicable of all
Awesome Problem , I found very interesting Properties in this question ..
Okay , First Take advantage of fact given in question , Let A B = a & C D = b ,
Now Key is to Switch to co-ordinate geometry .. Let us choose sutaible co-ordinates for above stated conditions , D ( 0 , 0 ) & C ( b , 0 ) & A ( c , a ) & B ( c + a , a ) .
Note : I will repetedly use distance formula and square it in both sides
( i ) ∵ A C = C D ( c − b ) 2 + a 2 = b 2 c 2 + a 2 = 2 b c ( i i ) ∵ A D = B C ( ∵ I s o s c l a c e t r a p . ) c 2 + a 2 = ( c + a − b ) 2 + ( a ) 2 0 = 2 a c + ( a 2 + b 2 − 2 a b ) − 2 b c ( b − a ) 2 = 2 c ( b − a ) ( ∵ b = a ) b + a = 2 c
Now isn't it is beuatiful that a , c , b are in AP (Airthmetic Progression) ?
Now from above two conditions (on which i had putted Box) Put value of C from 2nd Box in to 1st box , and then we devide by b 2 to make quadaratic in a / b ..
∵ c 2 + a 2 = 2 b c 4 ( a + b ) 2 + a 2 = ( b + a ) b 5 a 2 + 2 a b − 3 b 2 = 0 b a = λ ( L e t ) 5 λ 2 + 2 λ − 3 = 0 λ = 5 3 , − 1 ( × ) b a = 5 3
@Brian Charlesworth , Isn't it is beautiful , that a , c , b are in AP . ?
Log in to reply
I think that you'll find that the equation in the second box should be b − a = 2 c , (which will mean that a , c , b are not in A.P.). You end up getting the same equation in λ in the end, however.
Since we end up with b = 3 5 a and c = 3 1 a I think that c , a , b are in A.P., though, which is indeed a beautiful result.
P.S., Nice solution method. :)
Without loss of generality let ∣ C D ∣ = 1 . Now let P be the point on C D that is the base of the altitude to vertex A . Letting ∣ A B ∣ = r , we have that
∣ D P ∣ = 2 1 ( 1 − r ) ⟹ ∣ P C ∣ = ∣ D C ∣ − ∣ D P ∣ = 1 − 2 1 ( 1 − r ) = 2 1 ( 1 + r ) .
Applying Pythagoras to Δ A P C , we find that
∣ A C ∣ 2 = ∣ A P ∣ 2 + ∣ P C ∣ 2 ⟹ 1 = r 2 + 4 1 ( 1 + r ) 2
⟹ 4 = 4 r 2 + 1 + 2 r + r 2 ⟹ 5 r 2 + 2 r − 3 = 0 ⟹ ( 5 r − 3 ) ( r + 1 ) = 0 .
Since r > 0 we find that r = ∣ A B ∣ = 5 3 . But with ∣ C D ∣ = 1 , r is the ratio we are wanting to find, and thus a b = 3 5 = 2 4 3 .
Can you confirm that the image I added is correct?
Log in to reply
Looks great. C D and A C don't look to have the same length in the diagram, but once people read the text of the question that won't be an issue. Thank you. :)
According to the convention that I was taught, the vertices must be named in a clockwise or counterclockwise fashion. I think that you placed C under (or over) A and D under (or over) B. The convention was taught in my school a few years ago and I don't know if it has changed now or if it was wrong from the beginning, but that caused my calculations to go wrong.
Log in to reply
So in the end, what I got was your quadratic equation, but with -2ab instead of +2ab. I think you ought to add a picture to make your question more understandable.
You're right; I had vertices C and D in the wrong order. I've edited the question accordingly. My intent was that the longer base was the same length as the diagonals. I'm sorry that my mistake prevented you from getting credit for answering the question. :( As for a diagram, I don't the capability to do that; perhaps one of the moderators will do so in time.
sir @Brian Charlesworth could you explain me why does not this agree...referring from the topmost figure given by sir @Niranjan Khanderia applying cosines law in triangle ADC from the fact that angle D is acute we get that (AC^2) = (AD^2) + (DC^2) -2(DC EC) now again we have (AC^2) = (AE^2) + (EC^2) so equating both of them we get (DE^2) + (DC^2) - 2(DC EC) = (EC^2) which can be re-written as (DE^2) + (DC^2) + (EC^2) - 2(DC*EC) = 2(EC^2) hence the equation translates into (DE^2) + (DC - EC)^2 = 2(EC^2) which yet again translates into 2(DE^2) = 2(EC^2) which implies DE = EC......which is absurd hence i had to go another way for the answer can you tell me where did i went astray..??
Nice solution
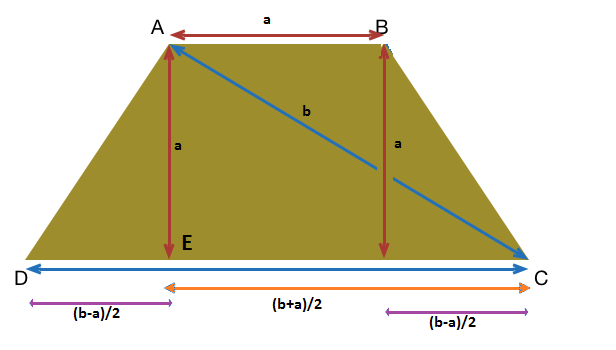
In right-angled △ E A C ,
a 2 + ( 2 b + a ) 2 = b 2
Divide both sides by b 2
⇒ ( b a ) 2 + 4 1 ( 1 + b a ) 2 = 1
let b a = α
⇒ α 2 + 4 1 ( 1 + α ) 2 = 1
⇒ 4 1 ( 1 + α ) 2 = 1 − α 2
Since α = − 1
⇒ 4 1 ( 1 + α ) = 1 − α
⇒ 1 + α = 4 − 4 α
⇒ α = 5 3
∴ a = 3 , b = 5 , and a b = 2 4 3
Hi, can you explain why do you use (b-a)/2?
From A drop a perpendicular onto D C and let it intersect D C at L . Drop another perpendicular from B onto D C and let it intersect D C at M .
So we have L M = A B
Now, C D = D L + L M + M C = 2 D L + A B implying D L = 2 C D − A B
So we now have, C L = C D − D L = 2 A B + C D
In the right Δ A L C ,
A C 2 = A L 2 + C L 2
Putting A C = C D and A L = A B in the above equation
C D 2 = A B 2 + ( 2 A B + C D ) 2
Divding both sides by C D 2 , taking y = C D A B and simplifying we get
5 y 2 + 2 y − 3 = 0
( 5 y − 3 ) ( y + 1 ) = 0
y = 5 3 (since y > 0 )
So we have b a = 5 3 so a b = 3 5 = 2 4 3
Just realized this is identical to your solution @Brian Charlesworth . Haha. :)
Log in to reply
Haha. No problem. Our solutions read a bit differently, and so some people may prefer you presentation to mine or visa versa. :)
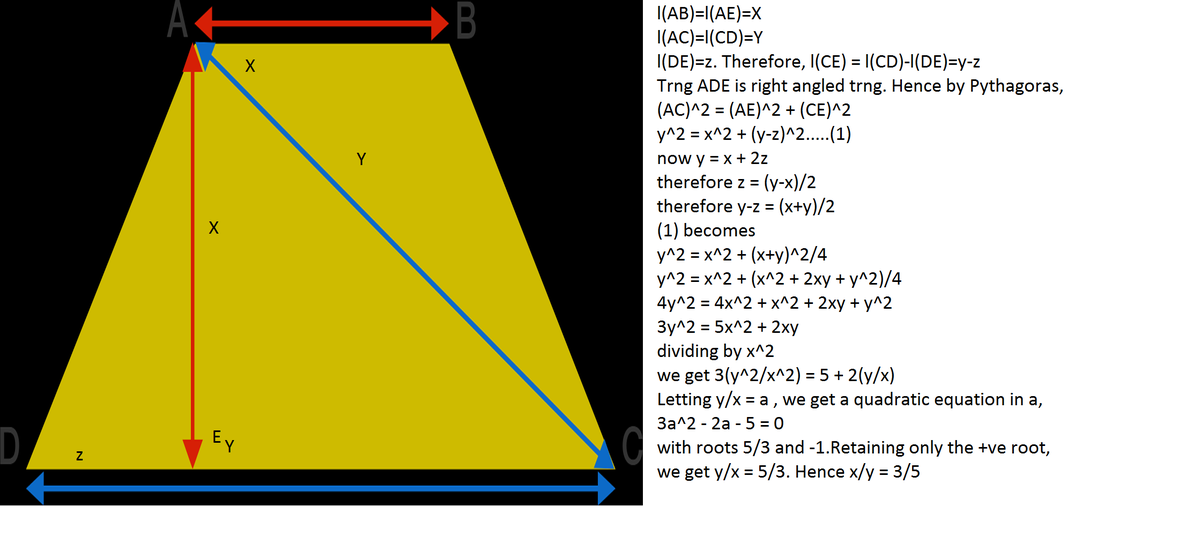
Sorry, it should be trng ACE and not ADE
Let ∣ A B ∣ = a and ∣ C D ∣ = b , therefore ∣ C D ∣ ∣ A B ∣ = b a , which is what we want to find. Let the foot of altitude from A to D C be E .
We note that ∣ A B ∣ = ∣ A E ∣ = a , ∣ C D ∣ = ∣ A C ∣ = b and ∣ C E ∣ = b − 2 b − a = 2 b + a .
We also note that
∣ C E ∣ 2 + ∣ A E ∣ 2 = ∣ A C ∣ 2 ⇒ ( 2 b + a ) 2 + a 2 = b 2 ⇒ b 2 + 2 a b + a 2 + 4 a 2 = 4 b 2 ⇒ 3 b 2 − 2 a b − 5 a 2 = 0 ⇒ ( 3 b − 5 a ) ( b + a ) = 0 ⇒ 3 b = 5 a ⇒ b a = 5 3 ⇒ a b = 3 5 = 2 4 3
